Alexander Ilich September 22, 2022
Please cite as
Ilich, Alexander R.; Misiuk, Benjamin; Lecours, Vincent; Murawski, Steven A.; 2021. “MultiscaleDTM”, https://doi.org/10.5281/zenodo.5548338. https://github.com/ailich/MultiscaleDTM.
This package calculates multi-scale geomorphometric terrain attributes from regularly gridded digital terrain models (DTM; i.e. elevation or bathymetry rasters) via a specified window size.
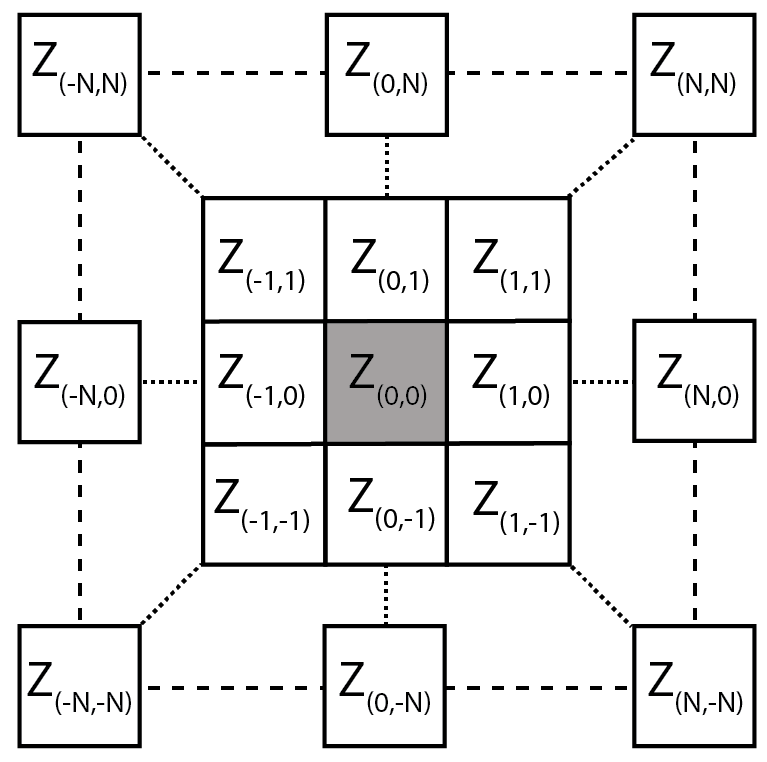
Figure adapted from Wilson et al. (2007)
If you don’t already have remotes installed, use the code
install.packages("remotes")
Then to install this package use the code
remotes::install_github("ailich/MultiscaleDTM") (If you are
using Windows, you may need to install Rtools using the instructions
found here).
This package relies on the terra package for handling of
spatial raster data.
SlpAsp calculates multi-scale slope and aspect
according to Misiuk et al (2021) which is a modification of the
traditional 3 x 3 slope and aspect algorithms (Fleming and Hoffer, 1979;
Horn et al., 1981; Ritter, 1987). This algorithm only considers a subset
of cells within the focal window, specifically the four cells on the
edge of the focal window directly up, down, left, and right of the focal
cell for the “rook” case and an additional four corner cells for the
“queen” case. 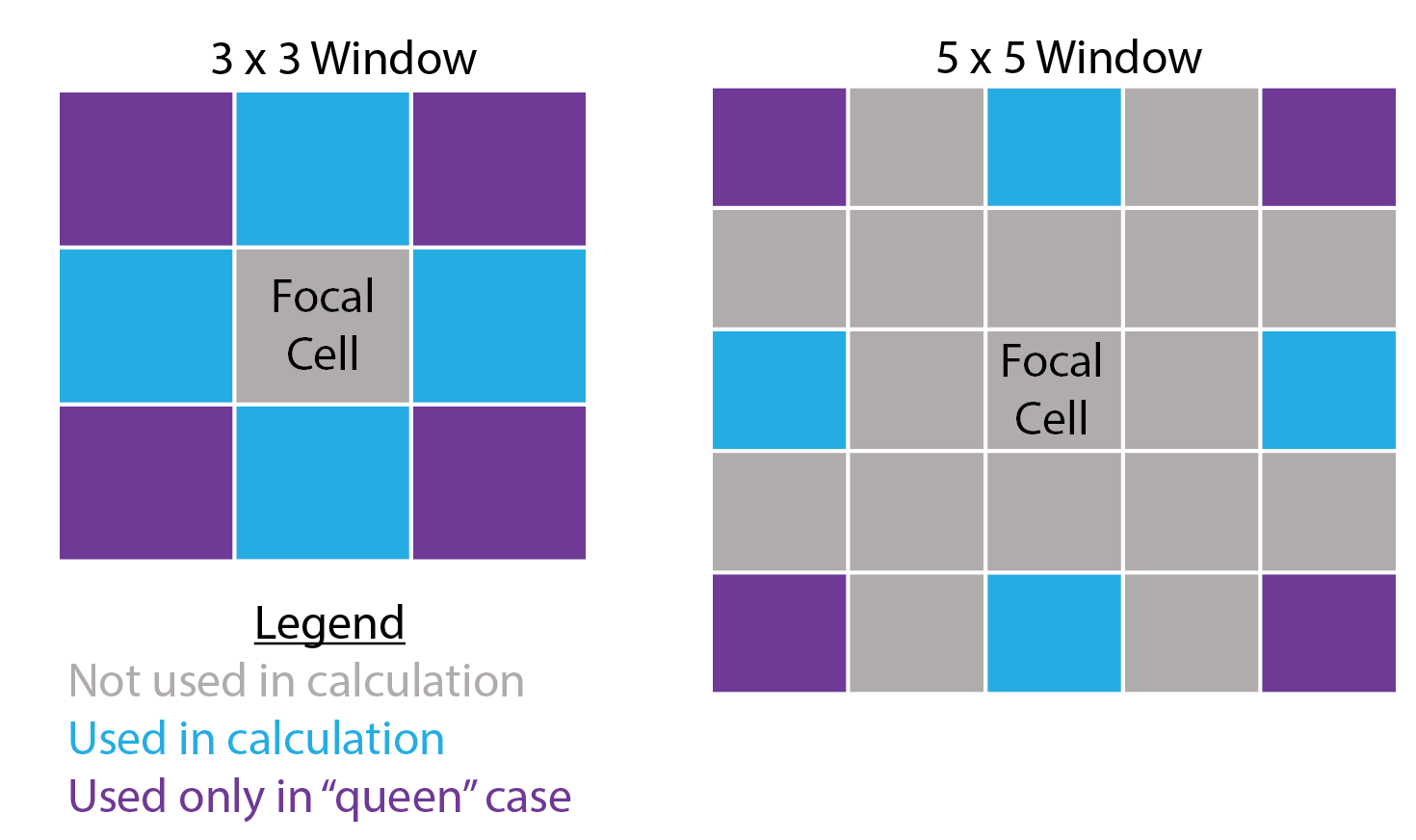
Qfit calculates slope, aspect, curvature, and
morphometric features by fitting a quadratic surface to the focal window
using ordinary least squares using the equation shown below where a-f
are regression parameters, Z is the elevation/depth, X is the east/west
coordinates in the focal window relative to the focal cell, and Y is the
north/south coordinates in the focal window relative to the focal cell
(Evans, 1980; Wilson et al., 2007; Wood, 1996). The morphometric
features algorithm has been modified to use more robust measures of
curvature based on the suggestions of Minár et al. (2020).
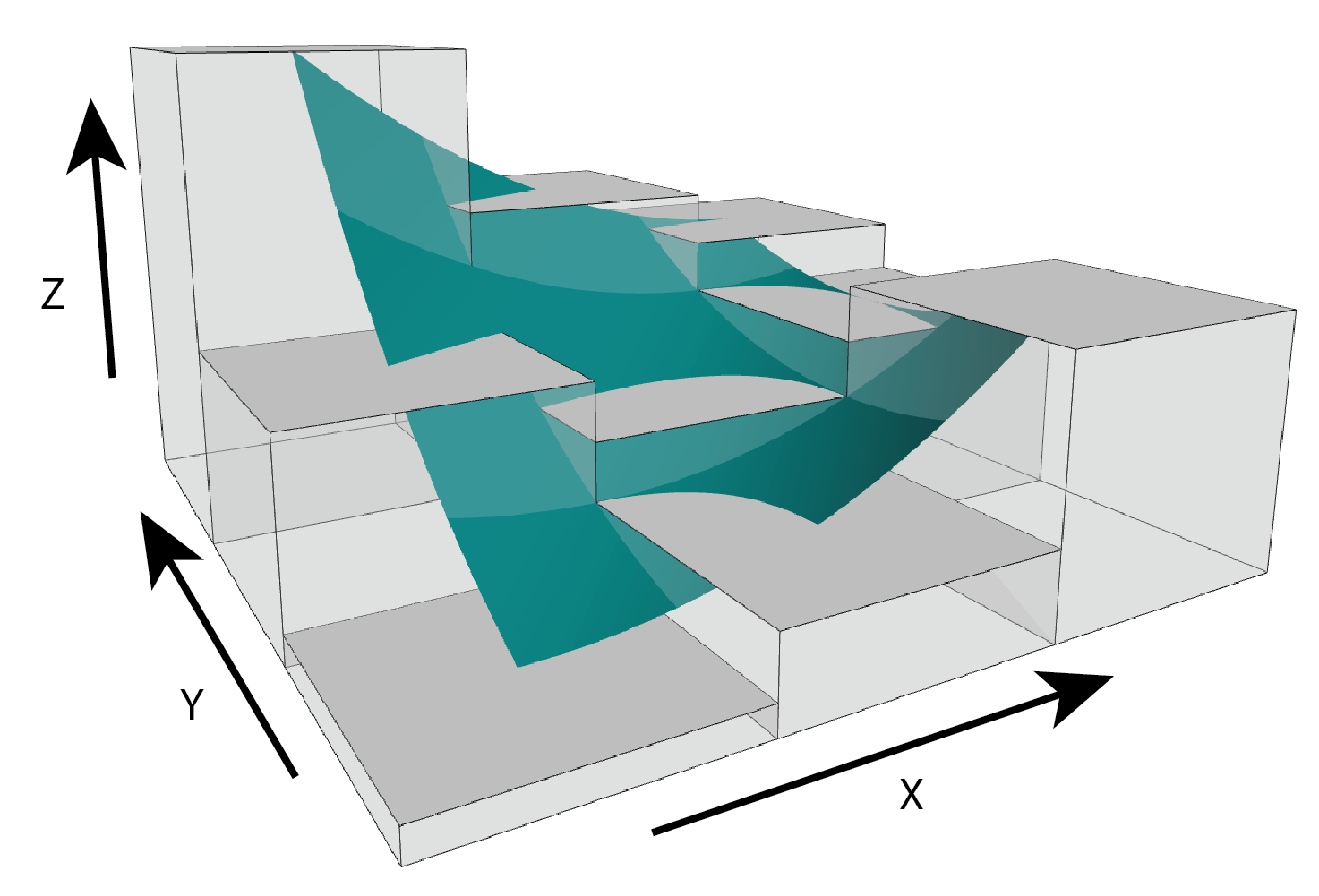
Figure adapted from Walbridge et al., (2018)
VRM - Vector ruggedness measure (Sappington et
al. 2007) quantifies terrain ruggedness by measuring the dispersion of
vectors normal to the terrain surface. This is accomplished by
calculating the local (3 x 3 cell) slope and aspect, and constructing
unit vectors normal to each cell in the DTM. These unit vectors are then
decomposed into their corresponding x, y, and z components (i.e. the x,
y, and z coordinates of the head of the vector relative to its origin)
and used in the following equation (note: n is the number of cells in
the window). VRM ranges from zero to one, representing completely smooth
to rugose surfaces, respectively. .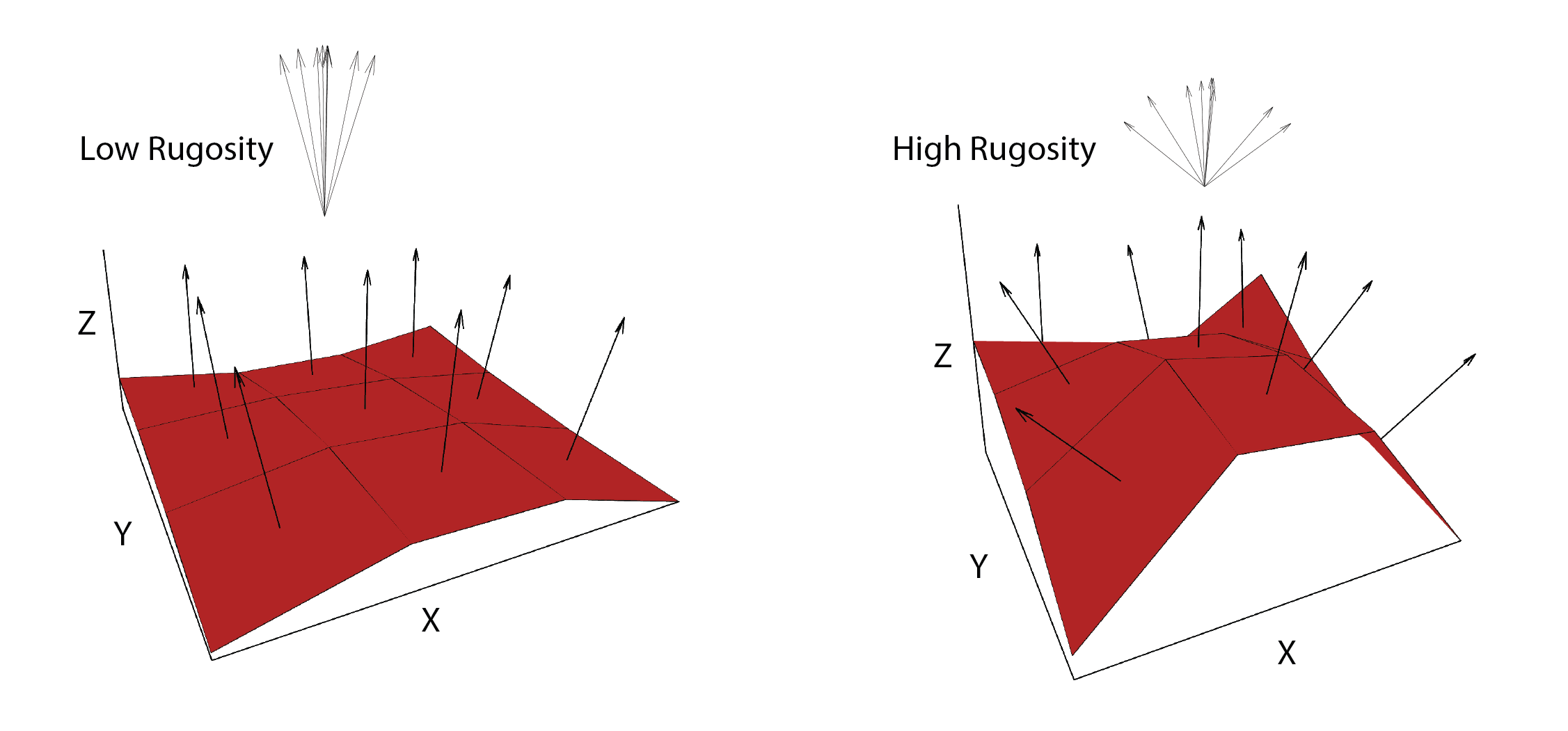
Figure adapted from Sappington et al. (2007)
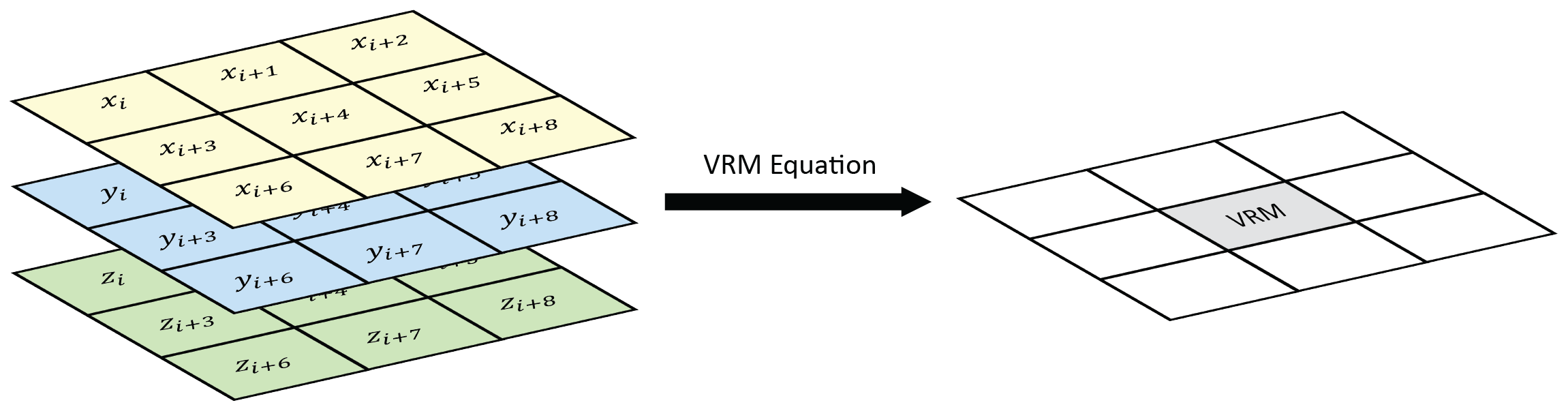
Figure adapted from Habib (2021)
SAPA - Calculates the Surface Area to Planar Area
(Jenness, 2004). More rugose surfaces will have a greater surface area
to planar area ratio, and perfectly smooth surfaces will have a value of
1. This is a 3D analog to the classical “chain-and-tape” method, which
calculates rugosity as the ratio of the contoured distance (chain
length) and linear distance (tape measure distance; Risk, 1972).
Additionally, planar area can be corrected for slope by dividing the
product of the x and y resolution by the cosine of slope (Du Preez
2015). Moreover, a proposed extension to multiple scales is provided by
summing the surface areas within the focal window and adjusting the
planar area of the focal window using multi-scale slope.
SurfaceArea - Calculate the surface area of each grid
cell (Jenness, 2004). This is accomplished by connecting a focal cell to
its immediate neighbors to create 8 large triangles. These large
triangles are then trimmed back to the extent of the focal cell using
the principle of similar triangles, and then the area of those 8 smaller
triangles are calculated and summed to estimate the surface area of the
focal pixel. This is used within SAPA.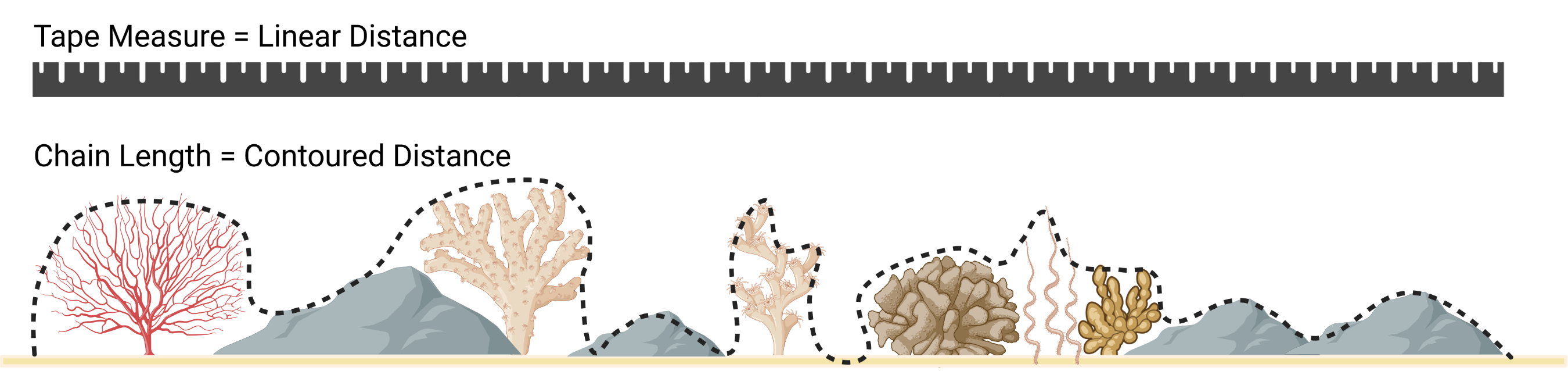
Figure adapted from Friedman et al. (2012) and created with BioRender.com.

Figure adapted from Jenness (2004)
AdjSD- This new proposed rugosity metric modifies the
standard deviation of elevation/bathymetry to account for slope. It does
this by first fitting a plane to the data in the focal window using
ordinary least squares, and then extracting the residuals, and then
calculating the standard deviation of the residuals within the focal
window.
RIE - Calculates the Roughness Index-Elevation which
quantifies the standard deviation of residual topography (Cavalli et
al., 2008). This measure is conceptually similar to AdjSD
but rather than fitting a plane and extracting residuals for the entire
focal window, residual topography is calculated as the focal pixel minus
the focal mean. Then the local standard deviation is calculated from
this residual topography using a focal filter.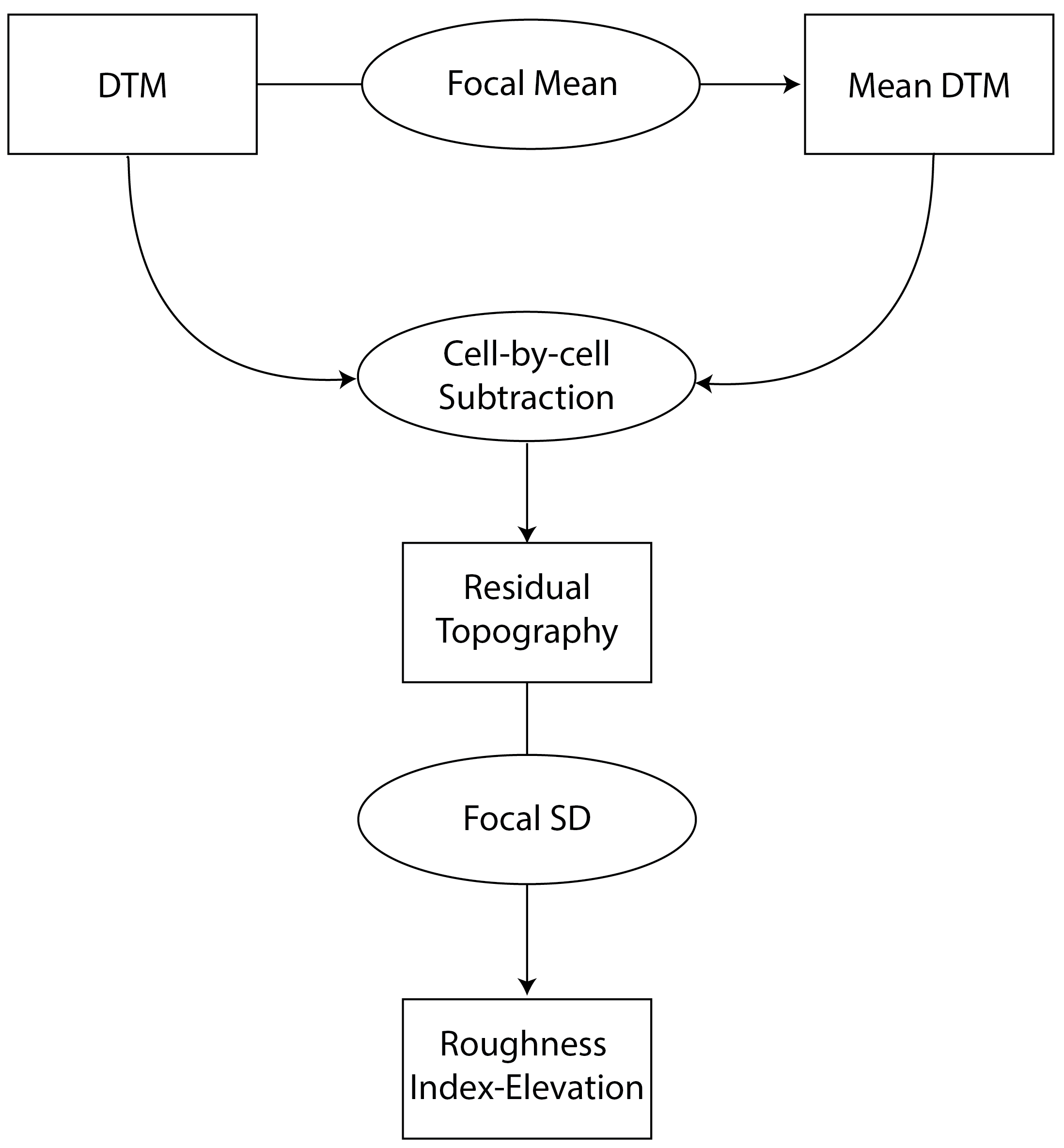
Figure adapted from Cavalli et al. (2008)
TPI - Topographic Position Index (Weiss, 2001) is
the difference between the value of a focal cell and the mean of the
surrounding cells.
RDMV - Relative Difference from Mean Value (Lecours
et al., 2017) is the difference between the value of a focal cell and
the mean of the cells in the focal window divided by the range or
standard deviation of the values in the focal window.
BPI - Bathymetric Position Index (Lundblad et al.,
2006) is the difference between the value of a focal cell and the mean
of the surrounding cells contained within an annulus shaped window. It
is a modification of TPI that uses an annulus shaped focal window and
therefore requires an inner and outer radius. For example, an annulus
window with an inner radius of 4 cells and an outer radius of 6 cells
would be

Figure adapted from Lundblad et al., (2006)
In this tutorial we will calculate various terrain attributes using a
5 x 5 cell rectangular window. Any rectangular odd numbered window size
however could be used (see figure directly below). Window sizes are
specified with a vector of length 2 of c(n_rows, n_cols).
If a single number is provided it will be used for both the number of
rows and columns. The only metric that does not follow this syntax is
BPI which uses an annulus shaped focal window which we will calculate
using an inner radius of 4 and an outer radius of 6 cells.
Load packages
library(MultiscaleDTM) #Load MultiscaleDTM packageSee package help page
help(package="MultiscaleDTM")Read in Data
r<- rast(volcano, extent= ext(2667400, 2667400 + ncol(volcano)*10, 6478700, 6478700 + nrow(volcano)*10), crs = "EPSG:27200")
slp_asp<- SlpAsp(r = r, w = c(5,5), unit = "degrees", method = "queen", metrics = c("slope", "aspect", "eastness", "northness"))
qmetrics<- Qfit(r, w = c(5,5), unit = "degrees", metrics = c("elev", "qslope", "qaspect", "qeastness", "qnorthness", "profc", "planc", "twistc", "meanc", "maxc", "minc", "features"), na.rm = TRUE)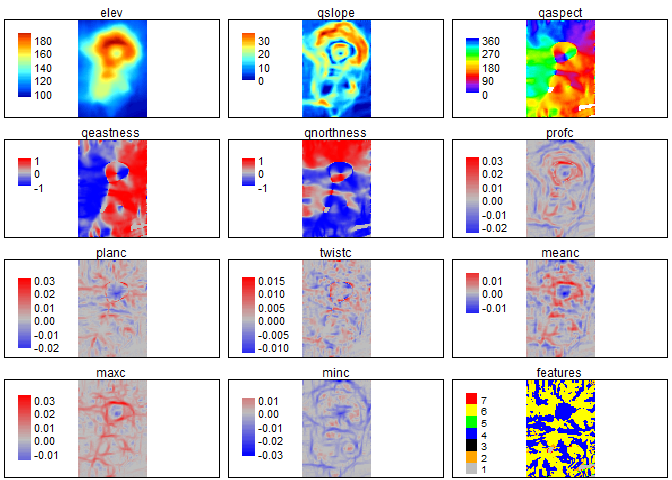
To explore these measures in an interactive environment use
explore_terrain() or go to this website
vrm<- VRM(r, w=c(5,5), na.rm = TRUE)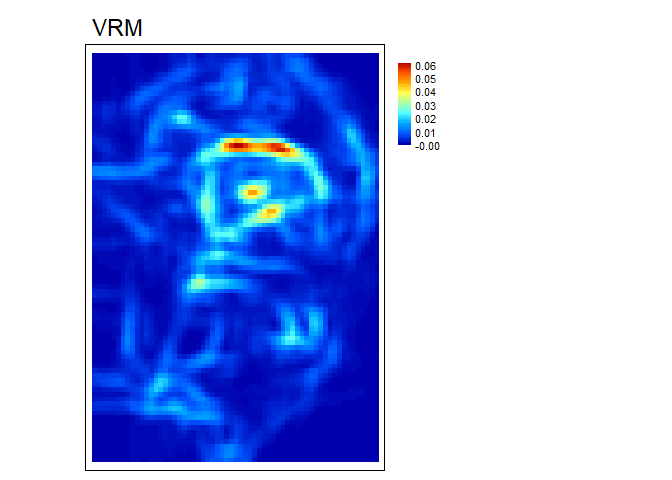
Note: multi-scale SAPA is experimental. The established metric by De
Preez (2015) would use w=1.
sapa<- SAPA(r, w=c(5,5), slope_correction = TRUE)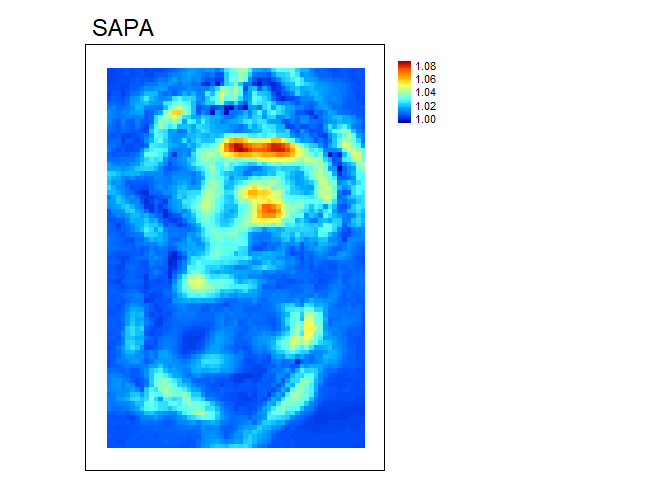
adj_SD<- AdjSD(r, w=c(5,5), na.rm = TRUE)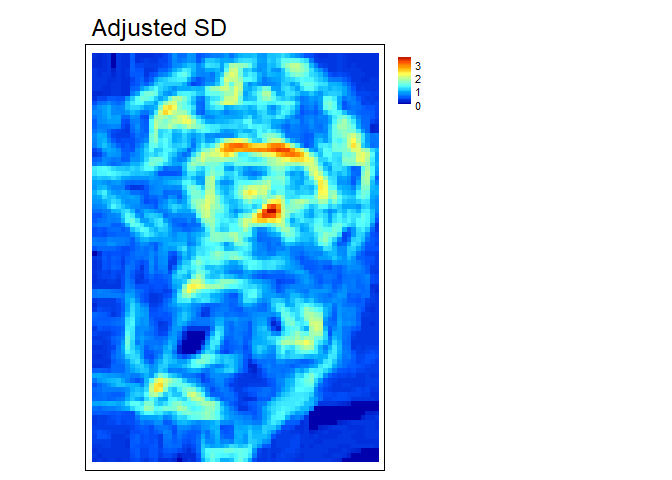
rie<- RIE(r, w=c(5,5), na.rm = TRUE)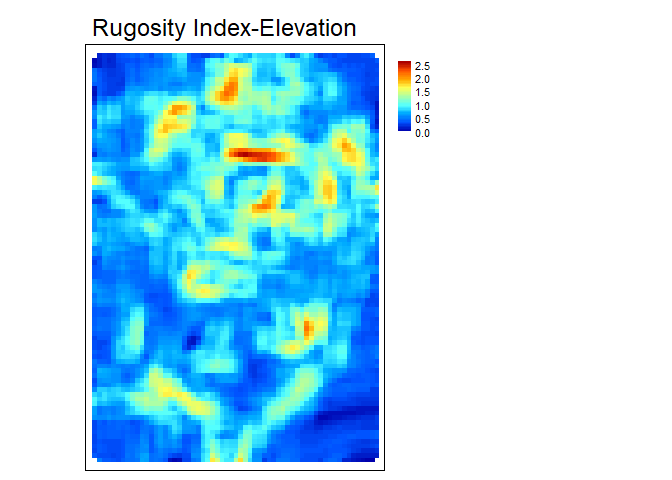
tpi<- TPI(r, w=c(5,5), na.rm = TRUE)
rdmv<- RDMV(r, w=c(5,5), na.rm = TRUE, method="range")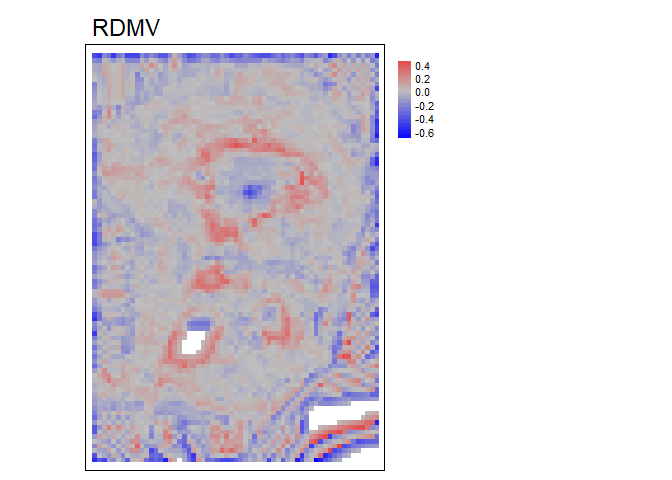
bpi<- BPI(r, radius = c(4,6), unit = "cell", na.rm = TRUE)
The annulus window for BPI can be specified in either cell units
(number of raster cells) or in map units (e.g. meters) which can be
useful if your x and y resolutions are not equal. Additionally, the
function annulus_window can be used to verify that you are
specifying your window correctly (NA’s are excluded cells and 1’s are
included cells) and can be directly supplied to the w
argument in the BPI funtion instead of using
radius and unit arguments.
annulus_window(radius = c(4,6), unit = "cell")## [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12] [,13]
## [1,] NA NA NA NA NA NA 1 NA NA NA NA NA NA
## [2,] NA NA NA 1 1 1 1 1 1 1 NA NA NA
## [3,] NA NA 1 1 1 1 1 1 1 1 1 NA NA
## [4,] NA 1 1 1 NA NA NA NA NA 1 1 1 NA
## [5,] NA 1 1 NA NA NA NA NA NA NA 1 1 NA
## [6,] NA 1 1 NA NA NA NA NA NA NA 1 1 NA
## [7,] 1 1 1 NA NA NA NA NA NA NA 1 1 1
## [8,] NA 1 1 NA NA NA NA NA NA NA 1 1 NA
## [9,] NA 1 1 NA NA NA NA NA NA NA 1 1 NA
## [10,] NA 1 1 1 NA NA NA NA NA 1 1 1 NA
## [11,] NA NA 1 1 1 1 1 1 1 1 1 NA NA
## [12,] NA NA NA 1 1 1 1 1 1 1 NA NA NA
## [13,] NA NA NA NA NA NA 1 NA NA NA NA NA NACavalli, M., Tarolli, P., Marchi, L., Dalla Fontana, G., 2008. The effectiveness of airborne LiDAR data in the recognition of channel-bed morphology. CATENA 73, 249–260. https://doi.org/10.1016/j.catena.2007.11.001
Du Preez, C., 2015. A new arc–chord ratio (ACR) rugosity index for quantifying three-dimensional landscape structural complexity. Landscape Ecol 30, 181–192. https://doi.org/10.1007/s10980-014-0118-8
Evans, I.S., 1980. An integrated system of terrain analysis and slope mapping. Zeitschrift f¨ur Geomorphologic Suppl-Bd 36, 274–295.
Fleming, M.D., Hoffer, R.M., 1979. Machine processing of landsat MSS data and DMA topographic data for forest cover type mapping (No. LARS Technical Report 062879). Laboratory for Applications of Remote Sensing, Purdue University, West Lafayette, Indiana.
Friedman, A., Pizarro, O., Williams, S.B., Johnson-Roberson, M., 2012. Multi-Scale Measures of Rugosity, Slope and Aspect from Benthic Stereo Image Reconstructions. PLOS ONE 7, e50440. https://doi.org/10.1371/journal.pone.0050440
Habib, M., 2021. Quantifying Topographic Ruggedness Using Principal Component Analysis. Advances in Civil Engineering 2021, e3311912. https://doi.org/10.1155/2021/3311912
Horn, B.K., 1981. Hill Shading and the Reflectance Map. Proceedings of the IEEE 69, 14–47.
Jenness, J.S., 2004. Calculating landscape surface area from digital elevation models. Wildlife Society Bulletin 32, 829–839. https://doi.org/10.2193/0091-7648(2004)032%5B0829:CLSAFD%5D2.0.CO;2
Lecours, V., Devillers, R., Simms, A.E., Lucieer, V.L., Brown, C.J., 2017. Towards a Framework for Terrain Attribute Selection in Environmental Studies. Environmental Modelling & Software 89, 19–30. https://doi.org/10.1016/j.envsoft.2016.11.027
Lundblad, E.R., Wright, D.J., Miller, J., Larkin, E.M., Rinehart, R., Naar, D.F., Donahue, B.T., Anderson, S.M., Battista, T., 2006. A benthic terrain classification scheme for American Samoa. Marine Geodesy 29, 89–111. https://doi.org/10.1080/01490410600738021
Minár, J., Evans, I.S., Jenčo, M., 2020. A comprehensive system of definitions of land surface (topographic) curvatures, with implications for their application in geoscience modelling and prediction. Earth-Science Reviews 211, 103414. https://doi.org/10.1016/j.earscirev.2020.103414
Misiuk, B., Lecours, V., Dolan, M.F.J., Robert, K., 2021. Evaluating the Suitability of Multi-Scale Terrain Attribute Calculation Approaches for Seabed Mapping Applications. Marine Geodesy 44, 327–385. https://doi.org/10.1080/01490419.2021.1925789
Risk, M.J., 1972. Fish Diversity on a Coral Reef in the Virgin Islands. Atoll Research Bulletin 153, 1–4. https://doi.org/10.5479/si.00775630.153.1
Ritter, P., 1987. A vector-based slope and aspect generation algorithm. Photogrammetric Engineering and Remote Sensing 53, 1109–1111.
Sappington, J.M., Longshore, K.M., Thompson, D.B., 2007. Quantifying Landscape Ruggedness for Animal Habitat Analysis: A Case Study Using Bighorn Sheep in the Mojave Desert. The Journal of Wildlife Management 71, 1419–1426. https://doi.org/10.2193/2005-723
Walbridge, S., Slocum, N., Pobuda, M., Wright, D.J., 2018. Unified geomorphological analysis workflows with benthic terrain modeler. Geosciences 8, 94. https://doi.org/10.3390/geosciences8030094
Weiss, A., 2001. Topographic Position and Landforms Analysis. Presented at the ESRI user conference, San Diego, CA.
Wilson, M.F., O’Connell, B., Brown, C., Guinan, J.C., Grehan, A.J., 2007. Multiscale Terrain Analysis of Multibeam Bathymetry Data for Habitat Mapping on the Continental Slope. Marine Geodesy 30, 3-35. https://doi.org/10.1080/01490410701295962
Wood, J., 1996. The geomorphological characterisation of digital elevation models (Ph.D.). University of Leicester.