README

This package implements a spectral approach to the parametric estimation of Hawkes processes from Binned Observations through Whittle likelihood (HawkesBOW). It is based on the results of the article (Cheysson and Lang 2020).

Installation

The Hawkes process

Hawkes processes form a family of models for point processes for which the occurrence of an event temporarily increases the probability of future events occurring (Hawkes 1971). Formally, a Hawkes process

can be defined from its conditional intensity $\lambda(\cdot)$ : where the variables

denote the arrival times of the process, the immigration intensity

is a positive constant, and the reproduction function $h: \mathbb R_{\ge 0} \rightarrow \mathbb R_{\ge 0}$ is a measurable function. The reproduction function can be further decomposed as $h = \mu h^\ast$ , where $\mu = \int_\mathbb R h(t) \mathrm{d} t < 1$ is called the and

is a true density function, $\int_\mathbb{R} h^\ast(t) \mathrm{d} t = 1$ , called the .

Alternatively, the Hawkes process can be constructed as a poissonian cluster process (Hawkes and Oakes 1974). The process consists of a flow of immigrants, the cluster centres, arriving according to a homogeneous Poisson process of intensity

. Then, an immigrant arriving at time

generates children according to an inhomogeneous Poisson process of intensity $h(\cdot - T_i)$ . These in turn independently generate children according to the same process, and so on ad infinitum. The processes consisting of an immigrant and all its descendants are therefore branching processes, and are independent of each other. 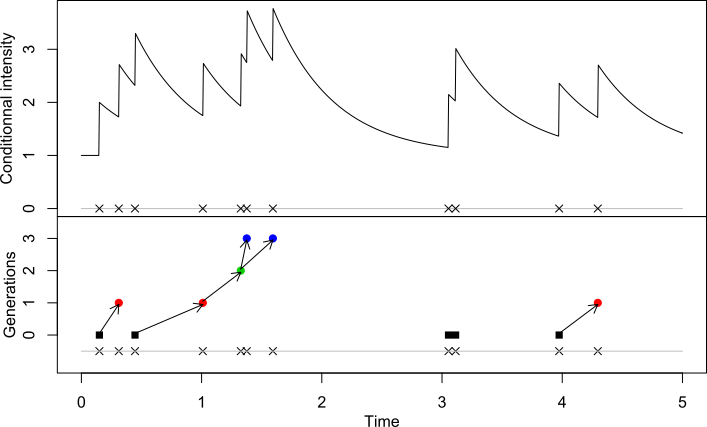Finally, the process resulting from the superposition of all these branching processes is a Hawkes process of conditional intensity $\lambda(\cdot)$ (see the following figure of a realisation of an exponential Hawkes process with $\\eta = 1$ ,

This package also supports non-causal Hawkes processes, for which the reproduction kernel

may take non-negative values on $\mathbb R_{\le 0}$ . Such processes are not defined through their conditional intensity functions, but through the poisson cluster representation, where each individual can potentially generate offsprings both in the future and in the past.

The count sequence of a Hawkes process is the time series generated by the event counts of the process, that is the series obtained by counting the events of the process on intervals of fixed length. Formally, the count sequence with bin size

associated to the point process

is the sequence $(X_k)_{k \in \mathbb Z}$ .

Estimation procedure

This package fully supports the parametric estimation of Hawkes processes from their count sequences via minimisation of the Whittle likelihood, and partially supports the estimation from the arrival times via maximisation of the likelihood.

Maximum likelihood estimation

The parameters of a Hawkes process with arrival times $(T_i)_{1\le i\le n}$ on the interval

can be estimated by maximising the following pseudo-likelihood
$\mathcal L_n(\theta) = \left( \prod_{i=1}^n \lambda(T_i) \right) \exp \left( - \int_0^T \lambda(s) \mathrm ds \right).$
Note that each step of the optimisation is usually of complexity $\mathcal O(n^2)$ .

Minimisation of the Whittle likelihood

Alternatively, the parameters of a Hawkes process with count sequence $(X_k)_{1\le k\le N}$ can be estimated by minimising the log-spectral (Whittle) likelihood
$\mathcal L_N^\prime(\theta) = \frac{1}{4\pi} \int_{-\pi}^\pi \left( \log f_\theta(\omega) + \frac{I_N(\omega)}{f_\theta(\omega)} \right) \mathrm d\omega,$
where $I_N(\omega) = (2\pi N)^{-1} \left| \sum_{k=1}^N X_k \exp(-ik\omega) \right|^2$ denotes the periodogram of

and $f_\theta(\cdot)$ its spectral density function. Note that each step of the optimisation is of complexity $\mathcal O(n)$ and the periodogram can be calculated in complexity $\mathcal O(n \log n)$ using a Fast Fourier Transform algorithm, making this method usually faster than maximum likelihood estimation.

Main usage

Simulation of Hawkes processes

where end denotes the end of the interval

. This function uses the cluster representation:

The argument fun can take a numeric value or be specified as a function, in which case the argument M must be specified as an upper bound on fun (to allow simulation of the immigration process by thinning). The argument family can either be specified as a string name corresponding to a distribution with random generation function rname (for example exp for rexp), or directly as a random generation function. The optional arguments ... are passed to the random generation function specified by family.

This returns a list of class hawkes, whose realisations are stored in the member p. Other members of the list are mainly used for support functions.

Examples

Plot function

If x is of class hawkes, as for objects returned by the function hawkes, arguments fun through M can be ignored. If intensity is set to FALSE, this plots the genealogy of the simulated Hawkes process (as in preceding figure, bottom panel). If it is set to TRUE, this plots the conditional intensity of the process (as in preceding figure, top panel).

Estimation of Hawkes processes

Two functions implement the estimation of Hawkes processes: mle from arrival times

and whittle from count sequences

. While the optimisation procedure rely on existing functions (see below), calculations of both the usual and Whittle likelihood functions are done in C++ via Rcpp (Eddelbuettel and François 2011) and RcppArmadillo (Eddelbuettel and Sanderson 2014).

By maximum likelihood

events holds the arrival times

in ascending order, kern must be a string (partially) matching one of the reproduction kernels (see below) and end denotes the endpoint

of observation of the process.

The optimisation of the maximum likelihood function is done by the function nloptr from the package nloptr (Johnson, n.d.) with algorithm L-BFGS-B, where the derivatives of the likelihood are calculated explicitly. By default, parameters are constrained to be positive, and additionally

is constrained to be below 1. However, both the arguments opts and ... are passed on to nloptr, so the algorithm, the constraints, or any other parameter of the optimisation procedure can be changed.

By minimisation of the Whittle likelihood

counts holds the count sequence

, kern must be a string (partially) matching one of the reproduction kernels (see below), binsize denotes the bin size

and trunc is the number of foldings due to aliasing taken into account.

The optimisation of the Whittle likelihood function is done by the function optim, with algorithm L-BFGS-B where the derivatives of the likelihood are approximated by finite differences. By default, parameters are constrained to be positive, and additionally

is constrained to be below 1. However, the argument ... is passed to optim, so any optimisation parameter can be changed.

Note that discrete is a useful function to create the count sequence

associated with an object x of class hawkes.

Reproduction kernels

We introduce the reproduction kernels that are currently implemented in this package. Recall that the Fourier transform of a reproduction kernel is given by
$\widetilde {h^\ast}(\omega) = \int_\mathbb R \exp(-i\omega t) h(t) \mathrm dt,$
and that it is a Hermitian function $\widetilde {h^\ast}(-\omega) = \overline{\widetilde {h^\ast}(\omega)}$ .

The exponential kernel

This is the exponential density function with parameter $\beta > 0$ :
$h^\ast(t) = \beta e^{-\beta t} 1_{\{t > 0\}}.$
Its Fourier transform is
$\widetilde {h^\ast}(\omega) = \beta \frac{1}{\beta + i\omega} = \beta \frac{\beta - i \omega}{\beta^2 + \omega^2}.$

The exponential kernel can be specified with the string Exponential and the parameter $\beta$ with the usual argument rate. Both maximum and Whittle likelihood methods are fully implemented for exponential kernels. Moreover, the likelihood function is implemented in complexity $\mathcal O(n)$ , using the relations in (Ozaki and Ogata 1979).

The symmetric exponential kernel

This is a symmetrised version of the exponential density function with parameter $\beta > 0$ :
$h^\ast(t) = \frac 1 2 \beta e^{-\beta |t|}.$
Its Fourier transform is
$\widetilde {h^\ast}(\omega) = \frac{\beta2}{\beta2 + \omega^2}.$

The symmetric exponential kernel can be specified with the string SymmetricExponential and the parameter

with the argument rate. Only the Whittle likelihood method is implemented for symmetric exponential kernels. Note that it is a non-causal kernel, as $h^\ast(t) \ne 0$ for

The gaussian kernel

This is the gaussian density function with mean $\nu \in \mathbb R$ and variance $\sigma^2 > 0$ :
$h^\ast(t) = \frac{1}{\sigma \sqrt{2\pi}}\exp\left(-\frac{(t-\nu)2}{2\sigma2}\right).$
Its Fourier transform is
$\widetilde {h^\ast}(\omega) = \exp\left(-\frac{\sigma2\omega2}{2}-i\nu\omega\right).$

The gaussian kernel can be specified with the string Gaussian and its parameters

and

with the usual arguments mean and sd respectively. Only the Whittle likelihood method is implemented for gaussian kernels. Note that it is a non-causal kernel, as $h^\ast(t) \ne 0$ for

The power law kernel

This is a normalised and shifted power law function, with shape $\theta > 0$ and scale

:
$h^\ast(t) = \theta a^\theta (t+a)^{-\theta-1} 1_{\{\theta > 0 \}}.$
For positive $\omega$ , its Fourier transform is given by
$\widetilde{h_\theta^\ast}(\omega) = \theta \exp(i\omega a)E_{\theta + 1} (i\omega a),$
where $E_{\theta}(ix)$ denotes the integral
$E_{\theta}(ix) = \int_1^\infty t^{-\theta} \exp(-ixt) \mathrm dt.$
With successive integration by parts, this integral can be related to $E_{\theta’}(ix)$ , with $0 < \theta’ \le 1$ .

If $\theta’ = 1$ or equivalently $\theta \in \mathbb N_{\ne 0}$ , the integral

, called the exponential integral with imaginary argument, can be related the trigonometric integrals and calculated using Padé approximants (Rowe et al. 2015, Appendix B), accurate to better than

. The function E1_imaginary implements this approximation.

If $\theta’ < 1$ or equivalently $\theta \in \mathbb R \setminus \mathbb N$ , the integral $E_\theta(ix)$ can be related to the incomplete gamma function with imaginary argument
$\Gamma_i(x, \alpha) = \int_x^\infty t^{\alpha-1} e^{-it} \mathrm{d}t,$
where $0 < \alpha < 1$ . We implemented Taylor approximations of this integral, accurate to better than

, in the function inc_gamma_imag.

The power law kernel can be specified with the string PowerLaw and its parameters $\theta$ and

with the arguments shape and scale respectively. Both maximum and Whittle likelihood methods are implemented for power law kernels.

The Pareto kernels

This is the Pareto density function with shape $\theta > 0$ and scale

:
$h_\theta^\ast(t) = \theta a^\theta t^{-\theta - 1} 1_{\{t > a\}}.$
For positive $\omega$ , its Fourier transform is given by
$\widetilde{h_\theta^\ast}(\omega) = \theta E_{\theta + 1} (i\omega a),$
see above for the definition of $E_\theta(ix)$ .

Only Pareto kernels with fixed $\theta = 1$ ,

, and

have been implemented and can specified with the strings Pareto1, Pareto2 and Pareto3 respectively, with parameter

specified with the argument scale. Only the Whittle method is available for Pareto kernels.

To be implemented

References

Cheysson, Felix, and Gabriel Lang. 2020. “Strong mixing condition for Hawkes processes and application to Whittle estimation from count data.” arXiv, March. https://arxiv.org/abs/2003.04314.

Eddelbuettel, Dirk, and Romain François. 2011. “Rcpp : Seamless R and C++ Integration.” J. Stat. Softw. 40 (8): 1–18. https://doi.org/10.18637/jss.v040.i08.

Eddelbuettel, Dirk, and Conrad Sanderson. 2014. “RcppArmadillo: Accelerating R with High-Performance C++ Linear Algebra.” Computational Statistics and Data Analysis 71: 1054–63. http://dx.doi.org/10.1016/j.csda.2013.02.005.

Hawkes, Alan G. 1971. “Spectra of Some Self-Exciting and Mutually Exciting Point Processes.” Biometrika 58 (1): 83–90. https://doi.org/10.2307/2334319.

Hawkes, Alan G., and David Oakes. 1974. “A cluster process representation of a self-exciting process.” J. Appl. Probab. 11 (03): 493–503. https://doi.org/10.2307/3212693.

Johnson, Steven G. n.d. “The NLopt nonlinear-optimization package.”

Ozaki, T., and Yosihiko Ogata. 1979. “Maximum likelihood estimation of Hawkes’ self-exciting point processes.” Ann. Inst. Stat. Math. 31 (1): 145–55. https://doi.org/10.1007/BF02480272.

Paparoditis, Efstathios. 2000. “Spectral density based goodness-of-fit tests for time series models.” Scand. J. Stat. 27 (1): 143–76. https://doi.org/10.1111/1467-9469.00184.

Rowe, B. T. P., M. Jarvis, R. Mandelbaum, G. M. Bernstein, J. Bosch, M. Simet, J. E. Meyers, et al. 2015. “GalSim: The modular galaxy image simulation toolkit.” Astron. Comput. 10: 121–50. https://doi.org/10.1016/j.ascom.2015.02.002.

hawkesbow