A package for getting the most of our multilevel models in R
by Jared E. Knowles and Carl Frederick
Working with generalized linear mixed models (GLMM) and linear mixed
models (LMM) has become increasingly easy with advances in the
lme4 package. As we have found ourselves using these models
more and more within our work, we, the authors, have developed a set of
tools for simplifying and speeding up common tasks for interacting with
merMod objects from lme4. This package
provides those tools.
# development version
library(devtools)
install_github("jknowles/merTools")
# CRAN version
install.packages("merTools")subBoot now works with glmerMod objects as
wellreMargins a new function that allows the user to
marginalize the prediction over breaks in the distribution of random
effect distributions, see ?reMargins and the new
reMargins vignette (closes #73)merModList functions now
apply the Rubin correction for multiple imputationfixef and ranef generics for
merModList objectsfastdisp generic for merModListsummary generic for merModListprint generic for merModListmerModList including
examples and a new imputation vignettemodelInfo generic for merMod objects
that provides simple summary stats about a whole modelstd.error of a multiply
imputed merModList when calling
modelRandEffStatsREimpact where some column names in
newdata would prevent the prediction intervals from being
computed correctly. Users will now be warned.wiggle where documentation incorrectly
stated the arguments to the function and the documentation did not
describe function correctlySee NEWS.md for more details.
The easiest way to demo the features of this application is to use the bundled Shiny application which launches a number of the metrics here to aide in exploring the model. To do this:
library(merTools)
m1 <- lmer(y ~ service + lectage + studage + (1|d) + (1|s), data=InstEval)
shinyMer(m1, simData = InstEval[1:100, ]) # just try the first 100 rows of data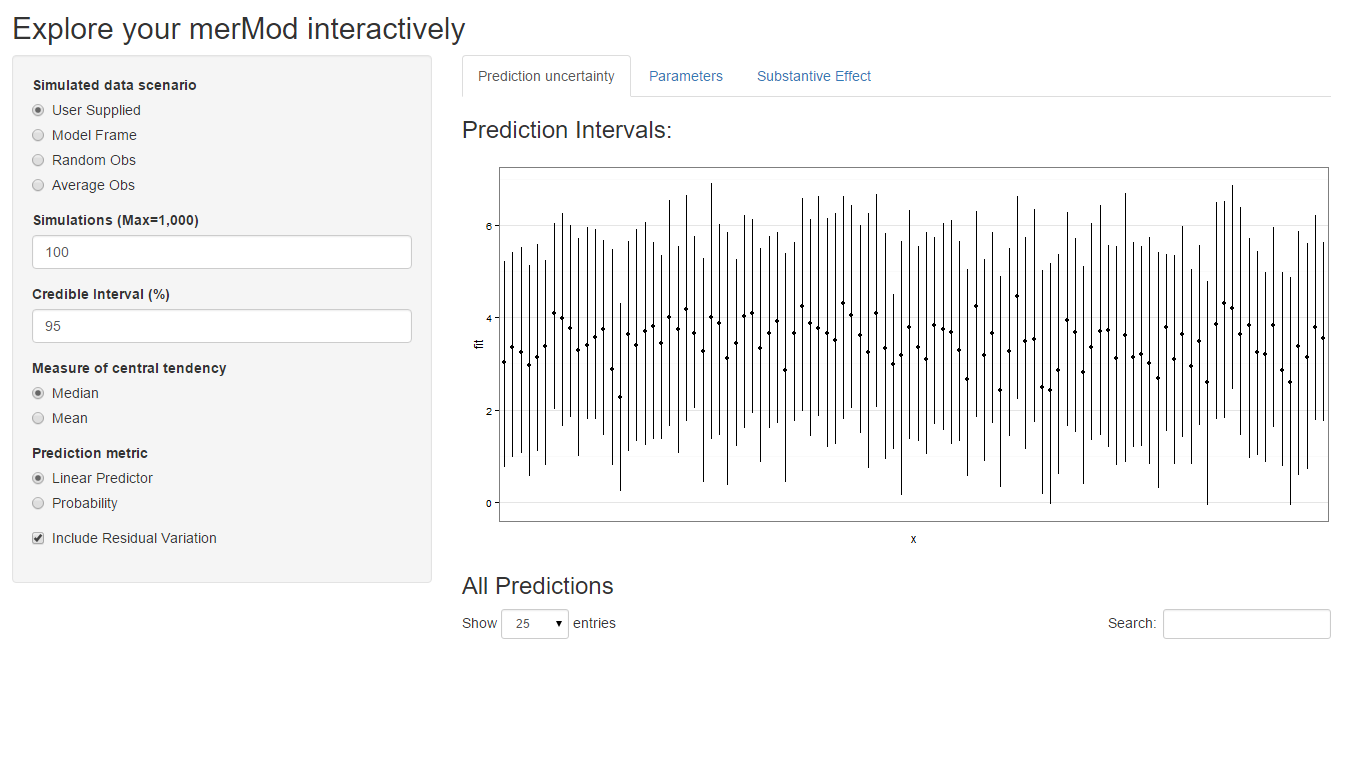
On the first tab, the function presents the prediction intervals for
the data selected by user which are calculated using the
predictInterval function within the package. This function
calculates prediction intervals quickly by sampling from the simulated
distribution of the fixed effect and random effect terms and combining
these simulated estimates to produce a distribution of predictions for
each observation. This allows prediction intervals to be generated from
very large models where the use of bootMer would not be
feasible computationally.
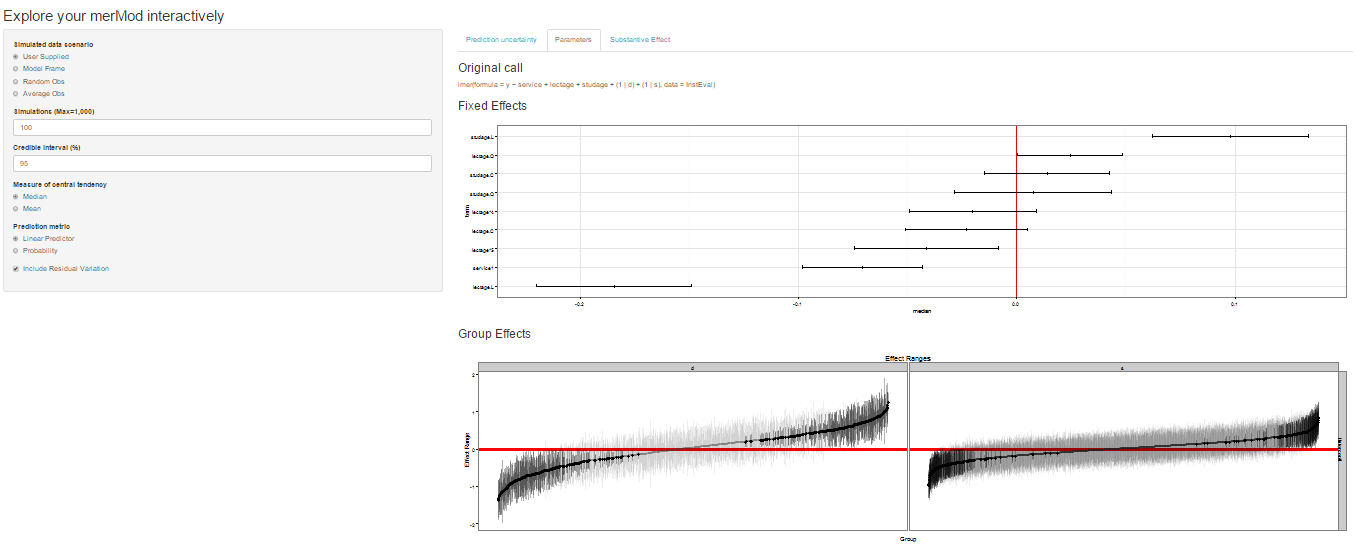
On the next tab the distribution of the fixed effect and group-level
effects is depicted on confidence interval plots. These are useful for
diagnostics and provide a way to inspect the relative magnitudes of
various parameters. This tab makes use of four related functions in
merTools: FEsim, plotFEsim,
REsim and plotREsim which are available to be
used on their own as well.
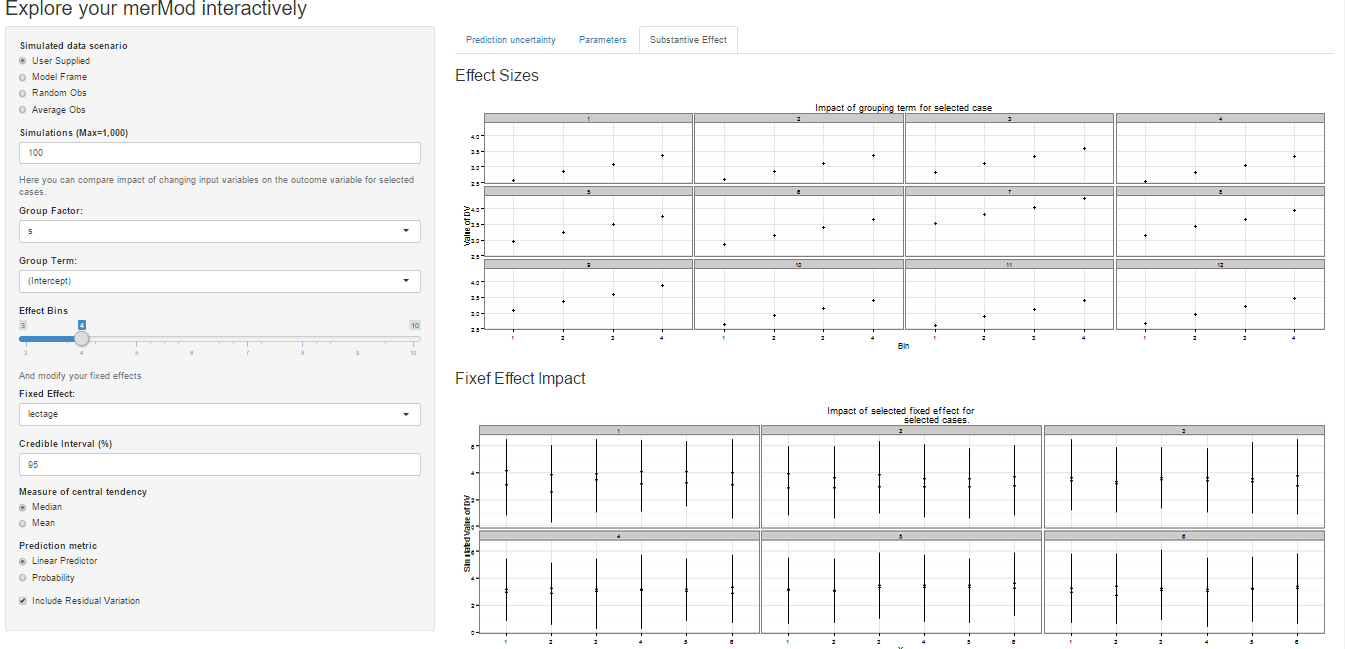
On the third tab are some convenient ways to show the influence or
magnitude of effects by leveraging the power of
predictInterval. For each case, up to 12, in the selected
data type, the user can view the impact of changing either one of the
fixed effect or one of the grouping level terms. Using the
REimpact function, each case is simulated with the model’s
prediction if all else was held equal, but the observation was moved
through the distribution of the fixed effect or the random effect term.
This is plotted on the scale of the dependent variable, which allows the
user to compare the magnitude of effects across variables, and also
between models on the same data.
Standard prediction looks like so.
predict(m1, newdata = InstEval[1:10, ])
#> 1 2 3 4 5 6 7 8
#> 3.146337 3.165212 3.398499 3.114249 3.320686 3.252670 4.180897 3.845219
#> 9 10
#> 3.779337 3.331013With predictInterval we obtain predictions that are more
like the standard objects produced by lm and
glm:
#predictInterval(m1, newdata = InstEval[1:10, ]) # all other parameters are optional
predictInterval(m1, newdata = InstEval[1:10, ], n.sims = 500, level = 0.9,
stat = 'median')
#> fit upr lwr
#> 1 3.015857 5.088929 1.1835562
#> 2 3.277143 5.220196 1.1038519
#> 3 3.404557 5.350846 1.3090942
#> 4 3.108511 5.314549 0.9256501
#> 5 3.260811 5.420831 1.2343590
#> 6 3.150673 5.267239 1.3318446
#> 7 4.085517 6.192887 2.1149662
#> 8 3.776922 5.715385 1.7600005
#> 9 3.799624 6.045041 1.7959515
#> 10 3.195235 5.180454 1.2971043Note that predictInterval is slower because it is
computing simulations. It can also return all of the simulated
yhat values as an attribute to the predict object
itself.
predictInterval uses the sim function from
the arm package heavily to draw the distributions of the
parameters of the model. It then combines these simulated values to
create a distribution of the yhat for each observation.
We can also explore the components of the prediction interval by
asking predictInterval to return specific components of the
prediction interval.
predictInterval(m1, newdata = InstEval[1:10, ], n.sims = 200, level = 0.9,
stat = 'median', which = "all")
#> effect fit upr lwr obs
#> 1 combined 3.18738014 4.966371 1.126030 1
#> 2 combined 2.97373166 5.126738 1.274230 2
#> 3 combined 3.27899702 5.362678 1.472948 3
#> 4 combined 3.23788384 5.020504 1.050771 4
#> 5 combined 3.37136338 5.350912 1.242096 5
#> 6 combined 3.15899583 5.217095 1.331035 6
#> 7 combined 4.14067417 6.187147 2.068142 7
#> 8 combined 4.02432057 6.067216 1.654789 8
#> 9 combined 3.77403216 5.554346 1.964592 9
#> 10 combined 3.42735845 5.296553 1.435939 10
#> 11 s 0.07251608 1.918014 -2.089567 1
#> 12 s 0.08247714 1.953635 -1.810187 2
#> 13 s 0.09157851 2.184732 -1.943005 3
#> 14 s 0.13788161 1.811599 -1.622534 4
#> 15 s 0.07322001 1.741112 -2.165038 5
#> 16 s -0.11882131 1.735864 -2.302783 6
#> 17 s 0.19512517 2.245456 -1.630585 7
#> 18 s 0.17986892 2.064228 -1.743939 8
#> 19 s 0.42961647 2.089356 -1.536597 9
#> 20 s 0.41084777 2.124038 -1.681811 10
#> 21 d -0.16574871 1.846935 -2.142487 1
#> 22 d -0.05194920 1.839777 -1.897692 2
#> 23 d 0.09294099 2.062341 -1.811622 3
#> 24 d -0.27500494 1.470227 -2.026380 4
#> 25 d 0.10836089 1.758614 -1.613323 5
#> 26 d -0.10553477 2.057018 -1.928175 6
#> 27 d 0.58243006 2.712166 -1.427938 7
#> 28 d 0.24593391 2.142436 -1.421031 8
#> 29 d 0.01724017 2.472836 -1.853576 9
#> 30 d -0.19182347 1.693597 -2.412778 10
#> 31 fixed 3.16933865 5.219839 1.287274 1
#> 32 fixed 3.16287615 5.140116 1.524180 2
#> 33 fixed 3.29291541 4.902726 1.382934 3
#> 34 fixed 3.01686447 5.285364 1.248745 4
#> 35 fixed 3.30761049 5.106185 1.420678 5
#> 36 fixed 3.32362576 4.872431 1.557399 6
#> 37 fixed 3.27480918 5.680335 1.374587 7
#> 38 fixed 3.47316648 5.063170 1.595717 8
#> 39 fixed 3.33332336 5.208318 1.435965 9
#> 40 fixed 3.27800249 5.158261 1.463540 10This can lead to some useful plotting:
library(ggplot2)
plotdf <- predictInterval(m1, newdata = InstEval[1:10, ], n.sims = 2000,
level = 0.9, stat = 'median', which = "all",
include.resid.var = FALSE)
plotdfb <- predictInterval(m1, newdata = InstEval[1:10, ], n.sims = 2000,
level = 0.9, stat = 'median', which = "all",
include.resid.var = TRUE)
plotdf <- dplyr::bind_rows(plotdf, plotdfb, .id = "residVar")
plotdf$residVar <- ifelse(plotdf$residVar == 1, "No Model Variance",
"Model Variance")
ggplot(plotdf, aes(x = obs, y = fit, ymin = lwr, ymax = upr)) +
geom_pointrange() +
geom_hline(yintercept = 0, color = I("red"), size = 1.1) +
scale_x_continuous(breaks = c(1, 10)) +
facet_grid(residVar~effect) + theme_bw()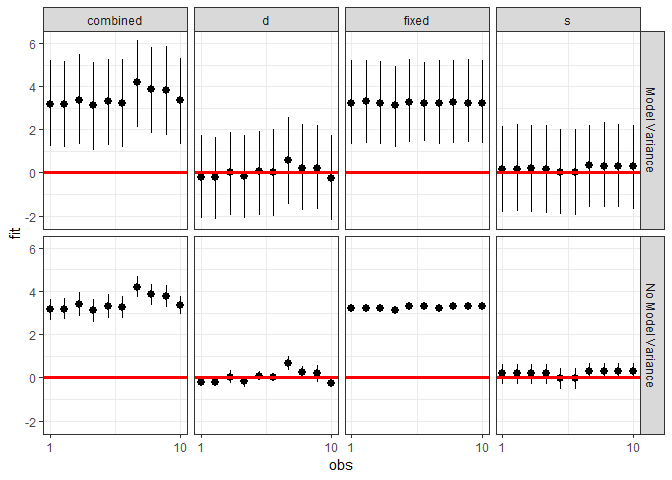
We can also investigate the makeup of the prediction for each observation.
ggplot(plotdf[plotdf$obs < 6,],
aes(x = effect, y = fit, ymin = lwr, ymax = upr)) +
geom_pointrange() +
geom_hline(yintercept = 0, color = I("red"), size = 1.1) +
facet_grid(residVar~obs) + theme_bw()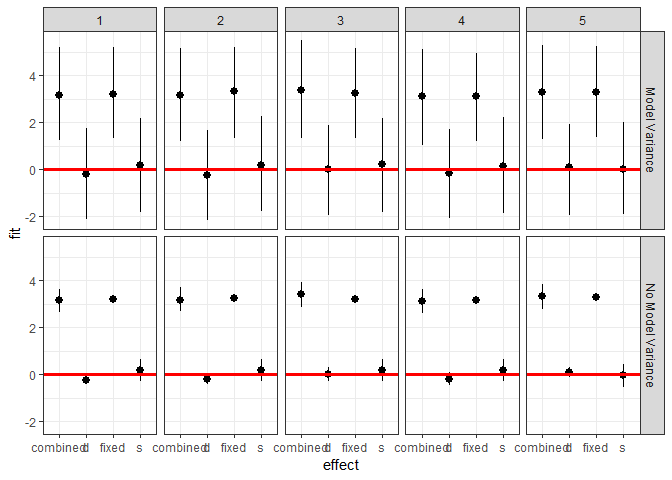
merTools also provides functionality for inspecting
merMod objects visually. The easiest are getting the
posterior distributions of both fixed and random effect parameters.
feSims <- FEsim(m1, n.sims = 100)
head(feSims)
#> term mean median sd
#> 1 (Intercept) 3.22450825 3.22391563 0.01814137
#> 2 service1 -0.07020093 -0.07020791 0.01288904
#> 3 lectage.L -0.18513512 -0.18608254 0.01616639
#> 4 lectage.Q 0.02471446 0.02512454 0.01087328
#> 5 lectage.C -0.02594511 -0.02425488 0.01300243
#> 6 lectage^4 -0.01880190 -0.01887871 0.01410205And we can also plot this:
plotFEsim(FEsim(m1, n.sims = 100), level = 0.9, stat = 'median', intercept = FALSE)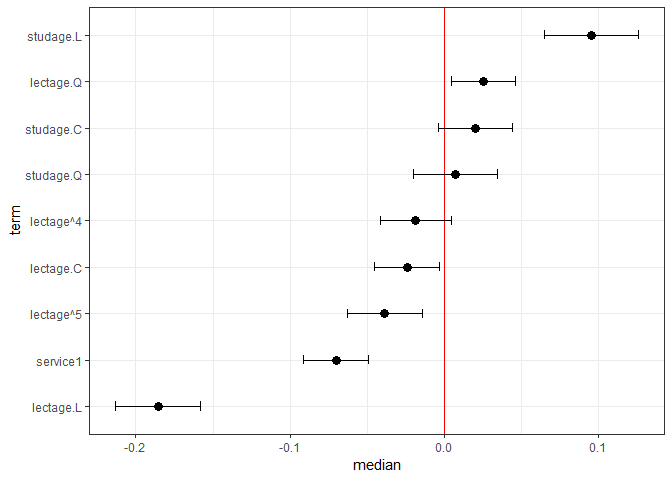
We can also quickly make caterpillar plots for the random-effect terms:
reSims <- REsim(m1, n.sims = 100)
head(reSims)
#> groupFctr groupID term mean median sd
#> 1 s 1 (Intercept) 0.21962903 0.26429668 0.3113619
#> 2 s 2 (Intercept) -0.04134078 -0.03064871 0.2922675
#> 3 s 3 (Intercept) 0.31819925 0.32744181 0.3530303
#> 4 s 4 (Intercept) 0.21088441 0.22023284 0.3176695
#> 5 s 5 (Intercept) 0.02441805 -0.02929245 0.3350150
#> 6 s 6 (Intercept) 0.10534748 0.12763830 0.2284094plotREsim(REsim(m1, n.sims = 100), stat = 'median', sd = TRUE)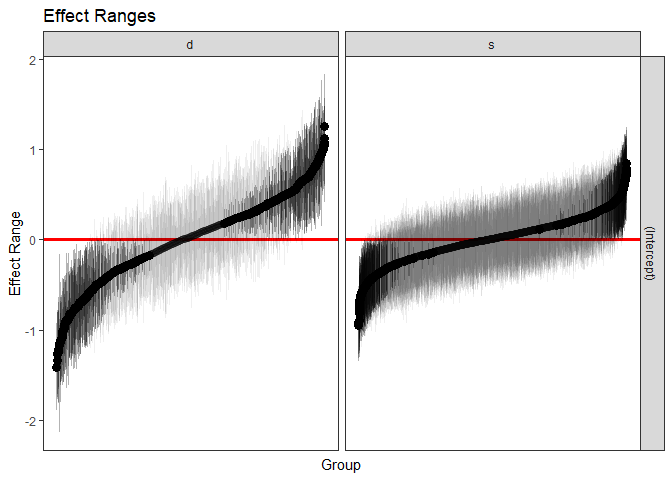
Note that plotREsim highlights group levels that have a
simulated distribution that does not overlap 0 – these appear darker.
The lighter bars represent grouping levels that are not distinguishable
from 0 in the data.
Sometimes the random effects can be hard to interpret and not all of
them are meaningfully different from zero. To help with this
merTools provides the expectedRank function,
which provides the percentile ranks for the observed groups in the
random effect distribution taking into account both the magnitude and
uncertainty of the estimated effect for each group.
ranks <- expectedRank(m1, groupFctr = "d")
head(ranks)
#> groupFctr groupLevel term estimate std.error ER pctER
#> 2 d 1 Intercept 0.3944919 0.08665152 835.3005 74
#> 3 d 6 Intercept -0.4428949 0.03901988 239.5363 21
#> 4 d 7 Intercept 0.6562681 0.03717200 997.3569 88
#> 5 d 8 Intercept -0.6430680 0.02210017 138.3445 12
#> 6 d 12 Intercept 0.1902940 0.04024063 702.3410 62
#> 7 d 13 Intercept 0.2497464 0.03216255 750.0174 66A nice features expectedRank is that you can return the
expected rank for all factors simultaneously and use them:
ranks <- expectedRank(m1)
head(ranks)
#> groupFctr groupLevel term estimate std.error ER pctER
#> 2 s 1 Intercept 0.16732800 0.08165665 1931.570 65
#> 3 s 2 Intercept -0.04409538 0.09234250 1368.160 46
#> 4 s 3 Intercept 0.30382219 0.05204082 2309.941 78
#> 5 s 4 Intercept 0.24756175 0.06641699 2151.828 72
#> 6 s 5 Intercept 0.05232329 0.08174130 1627.693 55
#> 7 s 6 Intercept 0.10191653 0.06648394 1772.548 60
ggplot(ranks, aes(x = term, y = estimate)) +
geom_violin(fill = "gray50") + facet_wrap(~groupFctr) +
theme_bw()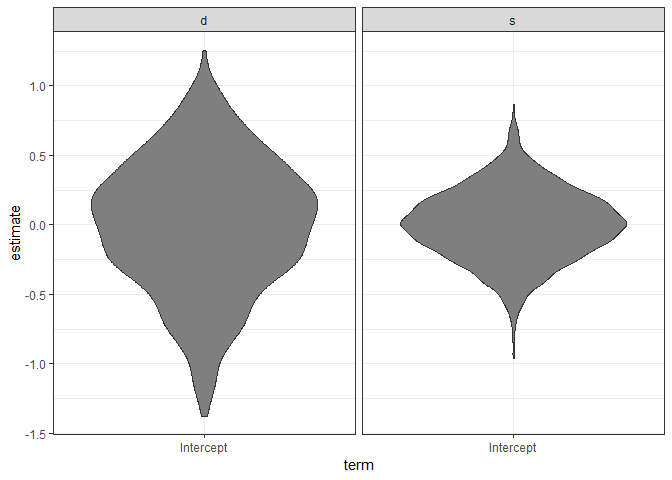
It can still be difficult to interpret the results of LMM and GLMM
models, especially the relative influence of varying parameters on the
predicted outcome. This is where the REimpact and the
wiggle functions in merTools can be handy.
impSim <- REimpact(m1, InstEval[7, ], groupFctr = "d", breaks = 5,
n.sims = 300, level = 0.9)
#> Warning: executing %dopar% sequentially: no parallel backend registered
impSim
#> case bin AvgFit AvgFitSE nobs
#> 1 1 1 2.797430 2.900363e-04 193
#> 2 1 2 3.263396 6.627139e-05 240
#> 3 1 3 3.551957 5.770126e-05 254
#> 4 1 4 3.841343 6.469439e-05 265
#> 5 1 5 4.236372 2.100511e-04 176The result of REimpact shows the change in the
yhat as the case we supplied to newdata is
moved from the first to the fifth quintile in terms of the magnitude of
the group factor coefficient. We can see here that the individual
professor effect has a strong impact on the outcome variable. This can
be shown graphically as well:
ggplot(impSim, aes(x = factor(bin), y = AvgFit, ymin = AvgFit - 1.96*AvgFitSE,
ymax = AvgFit + 1.96*AvgFitSE)) +
geom_pointrange() + theme_bw() + labs(x = "Bin of `d` term", y = "Predicted Fit")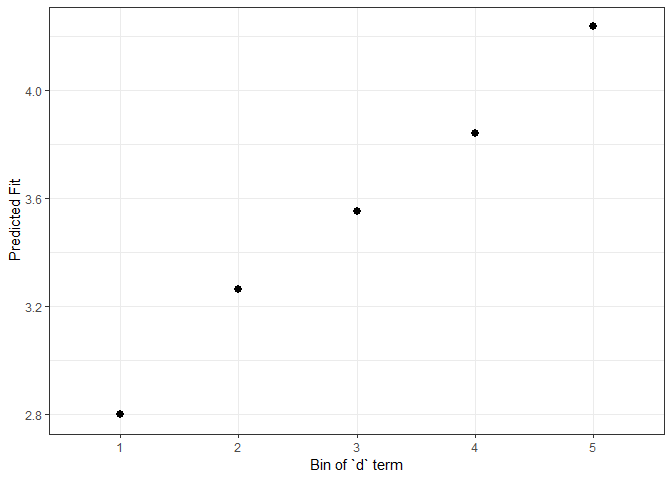
Here the standard error is a bit different – it is the weighted
standard error of the mean effect within the bin. It does not take into
account the variability within the effects of each observation in the
bin – accounting for this variation will be a future addition to
merTools.
Another feature of merTools is the ability to easily
generate hypothetical scenarios to explore the predicted outcomes of a
merMod object and understand what the model is saying in
terms of the outcome variable.
Let’s take the case where we want to explore the impact of a model with an interaction term between a category and a continuous predictor. First, we fit a model with interactions:
data(VerbAgg)
fmVA <- glmer(r2 ~ (Anger + Gender + btype + situ)^2 +
(1|id) + (1|item), family = binomial,
data = VerbAgg)
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl =
#> control$checkConv, : Model failed to converge with max|grad| = 0.0505464
#> (tol = 0.001, component 1)Now we prep the data using the draw function in
merTools. Here we draw the average observation from the
model frame. We then wiggle the data by expanding the
dataframe to include the same observation repeated but with different
values of the variable specified by the var parameter.
Here, we expand the dataset to all values of btype,
situ, and Anger subsequently.
# Select the average case
newData <- draw(fmVA, type = "average")
newData <- wiggle(newData, varlist = "btype",
valueslist = list(unique(VerbAgg$btype)))
newData <- wiggle(newData, var = "situ",
valueslist = list(unique(VerbAgg$situ)))
newData <- wiggle(newData, var = "Anger",
valueslist = list(unique(VerbAgg$Anger)))
head(newData, 10)
#> r2 Anger Gender btype situ id item
#> 1 N 20 F curse other 149 S3WantCurse
#> 2 N 20 F scold other 149 S3WantCurse
#> 3 N 20 F shout other 149 S3WantCurse
#> 4 N 20 F curse self 149 S3WantCurse
#> 5 N 20 F scold self 149 S3WantCurse
#> 6 N 20 F shout self 149 S3WantCurse
#> 7 N 11 F curse other 149 S3WantCurse
#> 8 N 11 F scold other 149 S3WantCurse
#> 9 N 11 F shout other 149 S3WantCurse
#> 10 N 11 F curse self 149 S3WantCurseThe next step is familiar – we simply pass this new dataset to
predictInterval in order to generate predictions for these
counterfactuals. Then we plot the predicted values against the
continuous variable, Anger, and facet and group on the two
categorical variables situ and btype
respectively.
plotdf <- predictInterval(fmVA, newdata = newData, type = "probability",
stat = "median", n.sims = 1000)
plotdf <- cbind(plotdf, newData)
ggplot(plotdf, aes(y = fit, x = Anger, color = btype, group = btype)) +
geom_point() + geom_smooth(aes(color = btype), method = "lm") +
facet_wrap(~situ) + theme_bw() +
labs(y = "Predicted Probability")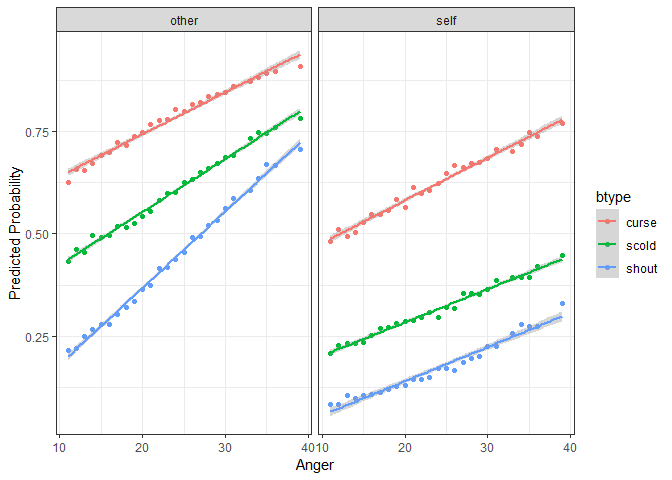
# get cases
case_idx <- sample(1:nrow(VerbAgg), 10)
mfx <- REmargins(fmVA, newdata = VerbAgg[case_idx,], breaks = 4, groupFctr = "item",
type = "probability")
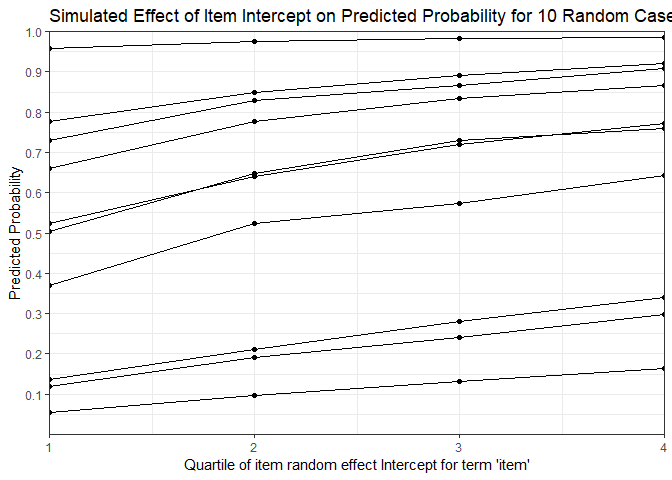
ggplot(mfx, aes(y = fit_combined, x = breaks, group = case)) +
geom_point() + geom_line() +
theme_bw() +
scale_y_continuous(breaks = 1:10/10, limits = c(0, 1)) +
coord_cartesian(expand = FALSE) +
labs(x = "Quartile of item random effect Intercept for term 'item'",
y = "Predicted Probability",
title = "Simulated Effect of Item Intercept on Predicted Probability for 10 Random Cases")