R package pomdp - Infrastructure for Partially Observable Markov Decision Processes (POMDP)

Provides the infrastructure to define and analyze the solutions of optimal control problems formulated as Partially Observable Markov Decision Processes (POMDP). The package uses the solvers from pomdp-solve (Cassandra, 2015) available in the R package pomdpSolve to solve POMDPs using a variety of algorithms.

The package provides the following algorithms:

• Exact value iteration
  • Enumeration algorithm (Sondik 1971, Mohan 1982).
  • Two pass algorithm (Sondik 1971).
  • Witness algorithm (Littman, Cassandra, Kaelbling 1996).
  • Incremental pruning algorithm (Zhang and Liu 1996, Cassandra et al 1997).
• Approximate value iteration
  • Finite grid algorithm (Cassandra 2015), a variation of point-based value iteration to solve larger POMDPs (PBVI; see Pineau 2003) without dynamic belief set expansion.
  • SARSOP (Kurniawati, Hsu and Lee 2008), point-based algorithm that approximates optimally reachable belief spaces for infinite-horizon problems (via package sarsop).

Installation

Stable CRAN version: Install from within R with

install.packages("pomdp")

Current development version: Install from r-universe.

install.packages("pomdp", repos = "https://mhahsler.r-universe.dev")

Usage

Solving the simple infinite-horizon Tiger problem.

library("pomdp")
data("Tiger")
Tiger

## POMDP, list - Tiger Problem
##   Discount factor: 0.75
##   Horizon: Inf epochs
##   List components: 'name', 'discount', 'horizon', 'states', 'actions',
##     'observations', 'transition_prob', 'observation_prob', 'reward',
##     'start', 'terminal_values'

sol <- solve_POMDP(model = Tiger)
sol

## POMDP, list - Tiger Problem
##   Discount factor: 0.75
##   Horizon: Inf epochs
##   Solved:
##     Solution converged: TRUE
##     Total expected reward: 1.933439
##   List components: 'name', 'discount', 'horizon', 'states', 'actions',
##     'observations', 'transition_prob', 'observation_prob', 'reward',
##     'start', 'solution', 'solver_output'

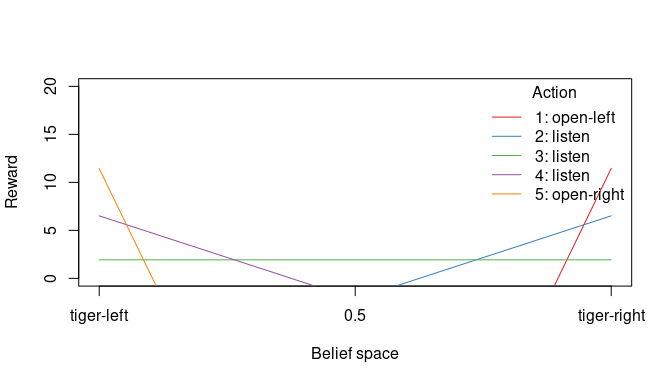
plot_value_function(sol, ylim = c(0, 20))

plot_policy_graph(sol)

References

• Cassandra, A. (2015). pomdp-solve: POMDP Solver Software, http://www.pomdp.org.
• Sondik, E. (1971). The Optimal Control of Partially Observable Markov Processes. Ph.D. Dissertation, Stanford University.
• Cassandra, A., Littman M.L., Zhang L. (1997). Incremental Pruning: A Simple, Fast, Exact Algorithm for Partially Observable Markov Decision Processes. UAI’97: Proceedings of the Thirteenth conference on Uncertainty in artificial intelligence, August 1997, pp. 54-61.
• Monahan, G. E. (1982). A survey of partially observable Markov decision processes: Theory, models, and algorithms. Management Science 28(1):1-16.
• Littman, M. L.; Cassandra, A. R.; and Kaelbling, L. P. (1996). Efficient dynamic-programming updates in partially observable Markov decision processes. Technical Report CS-95-19, Brown University, Providence, RI.
• Zhang, N. L., and Liu, W. (1996). Planning in stochastic domains: Problem characteristics and approximation. Technical Report HKUST-CS96-31, Department of Computer Science, Hong Kong University of Science and Technology.
• Pineau, J., Gordon, G.J., Thrun, S.B. (2003). Point-based value iteration: an anytime algorithm for POMDPs. IJCAI’03: Proceedings of the 18th international joint conference on Artificial Intelligence. Pages 1025-1030.
• Kurniawati, H., Hsu, D., and Lee, W.S. (2008). SARSOP: Efficient point-based POMDP planning by approximating optimally reachable belief spaces. In Proc. Robotics: Science and Systems.

Acknowledgments

Development of this package was supported in part by National Institute of Standards and Technology (NIST) under grant number 60NANB17D180.