

This package creates short sprint (<6sec) profiles using the split times, or the radar gun data. Mono-exponential equation is used to estimate maximal sprinting speed (MSS), relative acceleration (TAU), and other parameters. These parameters can be used to predict kinematic and kinetics variables and to compare individuals.
# Install from CRAN
install.packages("shorts")
# Or the development version from GitHub
# install.packages("devtools")
devtools::install_github("mladenjovanovic/shorts"){shorts} comes with two sample data sets: split_times
and radar_gun_data with N=5 athletes. Let’s load them
both:
require(shorts)
require(tidyverse)
require(knitr)
data("split_times", "radar_gun_data")To model sprint performance using split times, distance will be used
as predictor and time as target. Since split_times contains
data for multiple athletes, let’s extract only one athlete and model it
using shorts::model_timing_gates() function.
kimberley_data <- filter(split_times, athlete == "Kimberley")
kable(kimberley_data)| athlete | bodyweight | distance | time |
|---|---|---|---|
| Kimberley | 55 | 5 | 1.158 |
| Kimberley | 55 | 10 | 1.893 |
| Kimberley | 55 | 15 | 2.541 |
| Kimberley | 55 | 20 | 3.149 |
| Kimberley | 55 | 30 | 4.313 |
| Kimberley | 55 | 40 | 5.444 |
shorts::model_timing_gates() returns an object with
parameters, model_fit, model
returned from minpack.lm::nlsLM() function and
data used to estimate parameters. Parameters estimated
using mono-exponential equation are maximal sprinting speed
(MSS), and relative acceleration (TAU). Additional parameters
computed from MSS and TAU are maximal acceleration (MAC) and
maximal relative power (PMAX) (which is calculated as
MAC*MSS/4).
kimberley_profile <- shorts::model_timing_gates(
distance = kimberley_data$distance,
time = kimberley_data$time
)
kimberley_profile
#> Estimated model parameters
#> --------------------------
#> MSS TAU MAC PMAX
#> 8.59 0.81 10.59 22.74
#>
#> Model fit estimators
#> --------------------
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> 0.034 1.000 -0.053 0.027 0.053 0.028 0.023 1.193
summary(kimberley_profile)
#>
#> Formula: time ~ TAU * I(LambertW::W(-exp(1)^(-distance/(MSS * TAU) - 1))) +
#> distance/MSS + TAU
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> MSS 8.5911 0.1225 70.1 2.5e-07 ***
#> TAU 0.8113 0.0458 17.7 6.0e-05 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.034 on 4 degrees of freedom
#>
#> Number of iterations to convergence: 5
#> Achieved convergence tolerance: 1.49e-08
coef(kimberley_profile)
#> MSS TAU MAC PMAX
#> 8.59 0.81 10.59 22.74To return the predicted outcome (in this case time variable), use
predict() function:
predict(kimberley_profile)
#> [1] 1.2 1.9 2.5 3.1 4.3 5.5To create a simple plot, use S3 plot() method:
plot(kimberley_profile) +
theme_bw()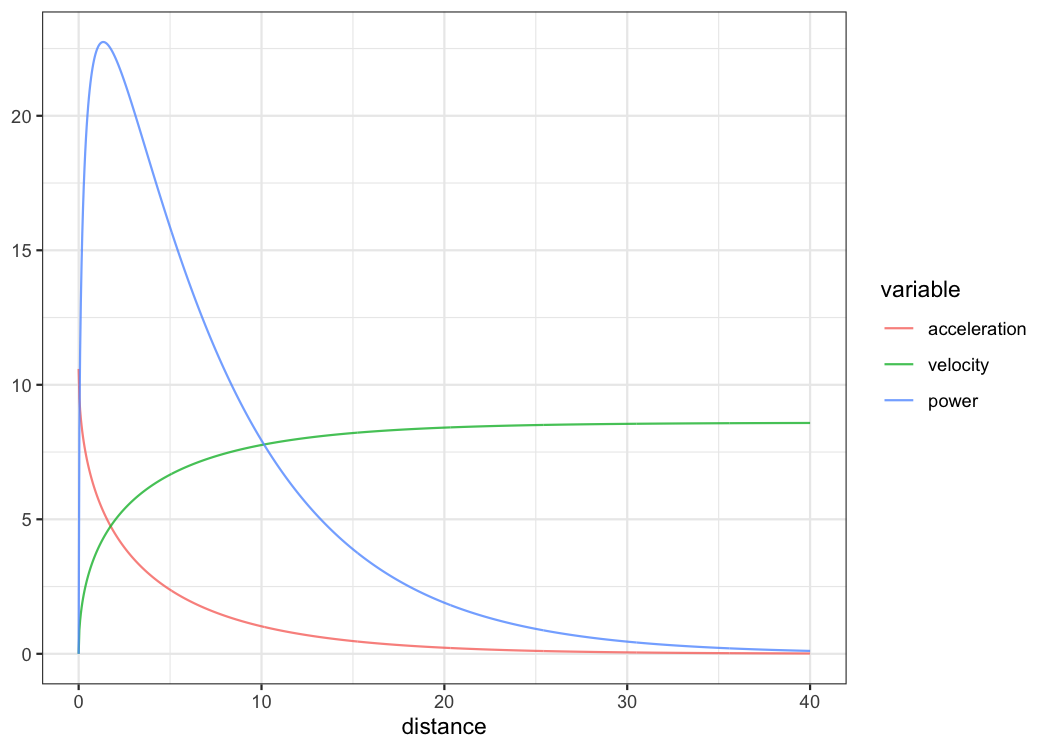
If you are interested in calculating average split velocity, use
shorts::format_splits()
kable(shorts::format_splits(
distance = kimberley_data$distance,
time = kimberley_data$time
))| split | split_distance_start | split_distance_stop | split_distance | split_time_start | split_time_stop | split_time | split_mean_velocity | split_mean_acceleration |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 5 | 5 | 0 | 1.158 | 1.158 | 4.317789…. | 3.728660…. |
| 2 | 5 | 10 | 5 | 1.158 | 1.893 | 0.735 | 6.802721…. | 3.380859…. |
| 3 | 10 | 15 | 5 | 1.893 | 2.541 | 0.648 | 7.716049…. | 1.409457…. |
| 4 | 15 | 20 | 5 | 2.541 | 3.149 | 0.608 | 8.223684…. | 0.834925…. |
| 5 | 20 | 30 | 10 | 3.149 | 4.313 | 1.164 | 8.591065…. | 0.315619…. |
| 6 | 30 | 40 | 10 | 4.313 | 5.444 | 1.131 | 8.841732…. | 0.221633…. |
Let’s plot observed vs fitted split times. For this we can use
data returned from
shorts::model_timing_gates() since it contains
pred_time column.
ggplot(kimberley_profile$data, aes(x = distance)) +
theme_bw() +
geom_point(aes(y = time)) +
geom_line(aes(y = pred_time)) +
xlab("Distance (m)") +
ylab("Time (s)")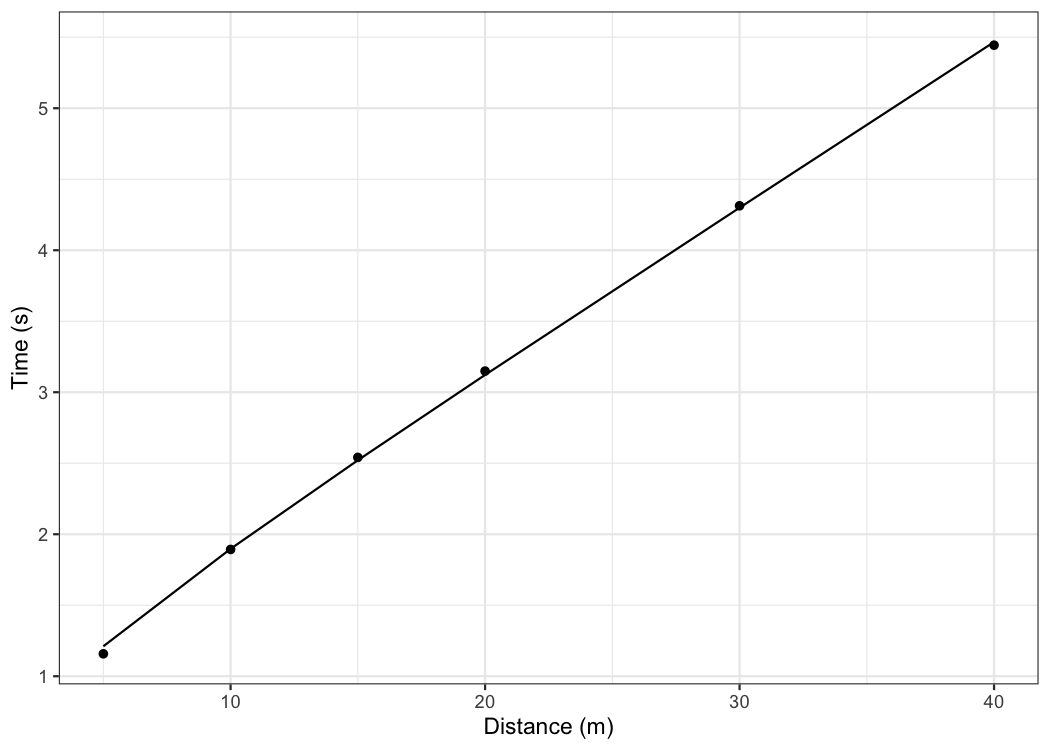
To plot predicted velocity, acceleration, air resistance, force, and
power over distance, use shorts:predict_XXX(). Please note
that to calculate force, air resistance, and power, we need Kimberley’s
bodymass and height (as well as other characteristics such as air
pressure, temperature and wind - see get_air_resistance()
function).
kimberley_bodymass <- 60 # in kilograms
kimberley_bodyheight <- 1.7 # in meters
kimberley_pred <- tibble(
distance = seq(0, 40, length.out = 1000),
# Velocity
pred_velocity = shorts::predict_velocity_at_distance(
distance,
kimberley_profile$parameters$MSS,
kimberley_profile$parameters$TAU
),
# Acceleration
pred_acceleration = shorts::predict_acceleration_at_distance(
distance,
kimberley_profile$parameters$MSS,
kimberley_profile$parameters$TAU
),
# Air resistance
pred_air_resistance = shorts::predict_air_resistance_at_distance(
distance,
kimberley_profile$parameters$MSS,
kimberley_profile$parameters$TAU,
bodymass = kimberley_bodymass,
bodyheight = kimberley_bodyheight
),
# Force
pred_force = shorts::predict_force_at_distance(
distance,
kimberley_profile$parameters$MSS,
kimberley_profile$parameters$TAU,
bodymass = kimberley_bodymass,
bodyheight = kimberley_bodyheight
),
# Power
pred_power = shorts::predict_power_at_distance(
distance,
kimberley_profile$parameters$MSS,
kimberley_profile$parameters$TAU,
bodymass = kimberley_bodymass,
bodyheight = kimberley_bodyheight
),
)
# Convert to long
kimberley_pred <- gather(kimberley_pred, "metric", "value", -distance)
ggplot(kimberley_pred, aes(x = distance, y = value)) +
theme_bw() +
geom_line() +
facet_wrap(~metric, scales = "free_y") +
xlab("Distance (m)") +
ylab(NULL)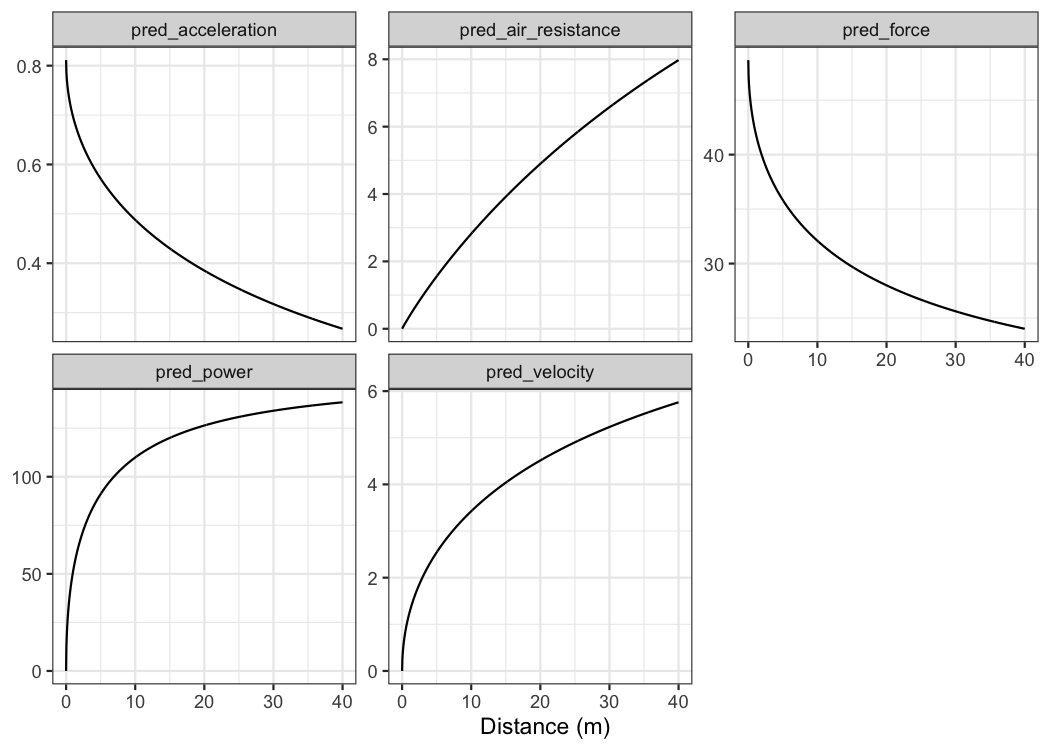
To do prediction simpler, use
shorts::predict_kinematics() function. This will provide
kinetics and kinematics for 0-6s sprint using 100Hz.
predicted_kinematics <- predict_kinematics(
kimberley_profile,
bodymass = kimberley_bodymass,
bodyheight = kimberley_bodyheight
)
kable(head(predicted_kinematics))| time | distance | velocity | acceleration | bodymass | net_horizontal_force | air_resistance | horizontal_force | horizontal_force_relative | vertical_force | resultant_force | resultant_force_relative | power | relative_power | RF | force_angle |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0.00 | 0.00 | 0.00 | 11 | 60 | 635 | 0.00 | 635 | 11 | 589 | 866 | 14 | 0 | 0.0 | 0.73 | 43 |
| 0.01 | 0.00 | 0.11 | 10 | 60 | 628 | 0.00 | 628 | 10 | 589 | 860 | 14 | 66 | 1.1 | 0.73 | 43 |
| 0.02 | 0.00 | 0.21 | 10 | 60 | 620 | 0.01 | 620 | 10 | 589 | 855 | 14 | 130 | 2.2 | 0.73 | 44 |
| 0.03 | 0.00 | 0.31 | 10 | 60 | 612 | 0.02 | 612 | 10 | 589 | 849 | 14 | 191 | 3.2 | 0.72 | 44 |
| 0.04 | 0.01 | 0.41 | 10 | 60 | 605 | 0.04 | 605 | 10 | 589 | 844 | 14 | 250 | 4.2 | 0.72 | 44 |
| 0.05 | 0.01 | 0.51 | 10 | 60 | 597 | 0.06 | 597 | 10 | 589 | 839 | 14 | 307 | 5.1 | 0.71 | 45 |
To get model residuals, use residuals() function:
residuals(kimberley_profile)
#> [1] -0.053 -0.004 0.020 0.027 0.014 -0.022Package {shorts} comes with find_XXX() family of
functions that allow finding peak power and it’s location, as well as
critical distance over which velocity, acceleration, or power
drops below certain threshold:
# Peak power and location
shorts::find_max_power_distance(
kimberley_profile$parameters$MSS,
kimberley_profile$parameters$TAU
)
#> $max_power
#> [1] 163
#>
#> $distance
#> [1] 30
# Distance over which power is over 50%
shorts::find_power_critical_distance(
MSS = kimberley_profile$parameters$MSS,
MAC = kimberley_profile$parameters$MAC,
percent = 0.5
)
#> $lower
#> [1] 0.086
#>
#> $upper
#> [1] 8.4
# Distance over which acceleration is under 50%
shorts::find_acceleration_critical_distance(
MSS = kimberley_profile$parameters$MSS,
MAC = kimberley_profile$parameters$MAC,
percent = 0.5
)
#> [1] 1.3
# Distance over which velocity is over 95%
shorts::find_velocity_critical_distance(
MSS = kimberley_profile$parameters$MSS,
MAC = kimberley_profile$parameters$MAC,
percent = 0.95
)
#> [1] 14The radar gun data is modeled using measured velocity as target
variable and time as predictor. Individual analysis is performed using
shorts::model_radar_gun() function. Let’s do analysis for
Jim:
jim_data <- filter(radar_gun_data, athlete == "Jim")
jim_profile <- shorts::model_radar_gun(
time = jim_data$time,
velocity = jim_data$velocity
)
jim_profile
#> Estimated model parameters
#> --------------------------
#> MSS TAU MAC PMAX TC
#> 8.0e+00 8.9e-01 9.0e+00 1.8e+01 1.1e-04
#>
#> Model fit estimators
#> --------------------
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> 0.051 0.999 -0.164 0.151 0.164 0.051 0.039 Inf
summary(jim_profile)
#>
#> Formula: velocity ~ MSS * (1 - exp(1)^(-(time + TC)/TAU))
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> MSS 7.99801 0.00319 2504.54 <2e-16 ***
#> TAU 0.88880 0.00218 407.81 <2e-16 ***
#> TC 0.00011 0.00123 0.09 0.93
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.051 on 597 degrees of freedom
#>
#> Number of iterations to convergence: 6
#> Achieved convergence tolerance: 1.49e-08
plot(jim_profile) +
theme_bw()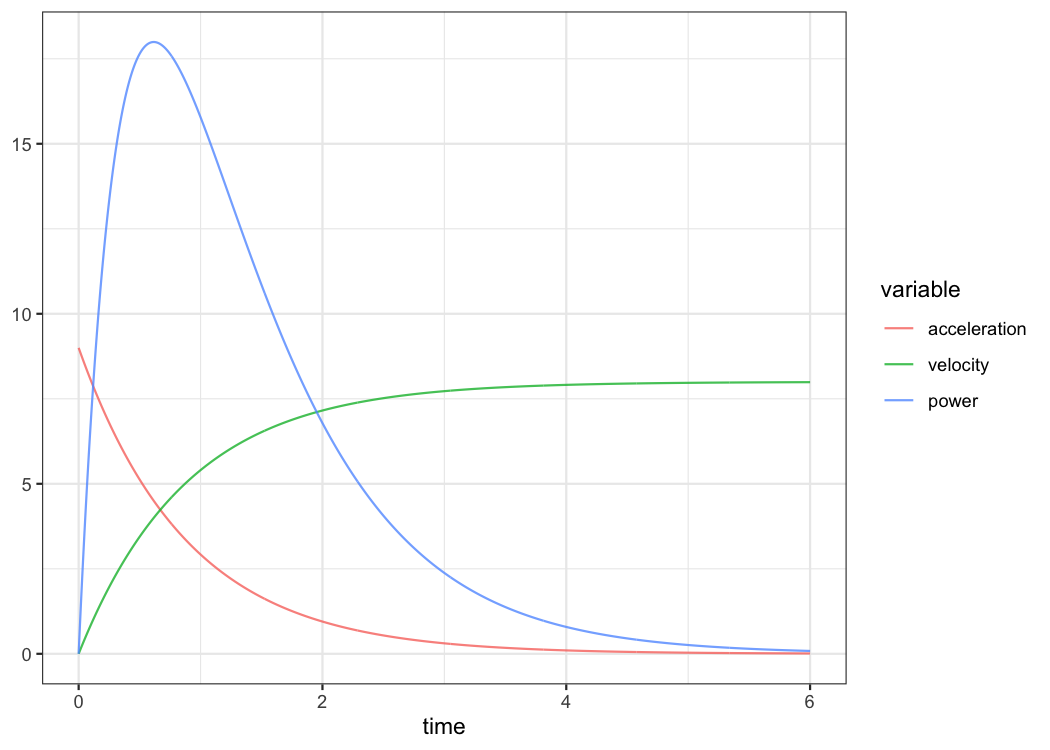
The object returned from shorts::model_radar_gun() is
same as object returned from shorts::model_timing_gates().
Let’s plot Jim’s measured velocity and predicted velocity:
ggplot(jim_profile$data, aes(x = time)) +
theme_bw() +
geom_line(aes(y = velocity), alpha = 0.5) +
geom_line(aes(y = pred_velocity), color = "red", alpha = 0.5) +
xlab("Time (s)") +
ylab("Velocity (m/s)")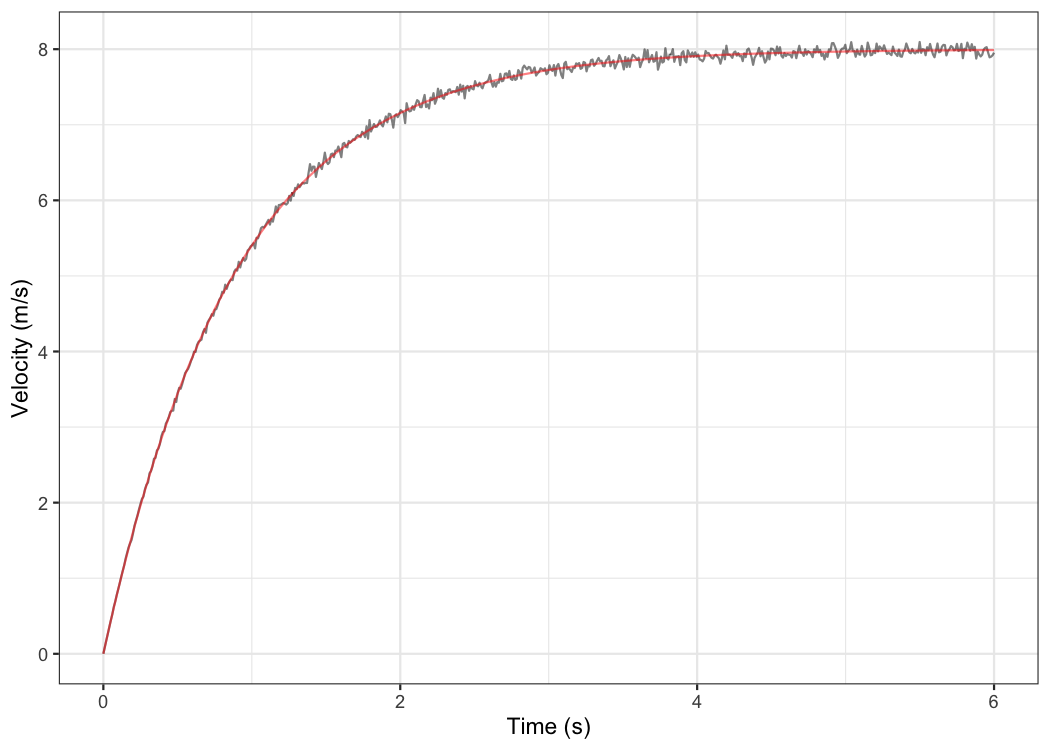
Some tether devices provide data out in a velocity-at-distance
format. In this case, velocity is the outcome variable and distance is
the predictor. To estimate sprint profiles from tether data,
use model_tether() function:
distance <- c(5, 10, 20, 30, 40)
velocity <- predict_velocity_at_distance(distance, MSS = 10, MAC = 8) +
rnorm(length(distance), 0, 0.1)
m1 <- model_tether(distance = distance, velocity = velocity)
df <- data.frame(
distance = distance,
obs_velocity = velocity
)
plot(m1) +
geom_point(data = df, aes(x = distance, y = obs_velocity))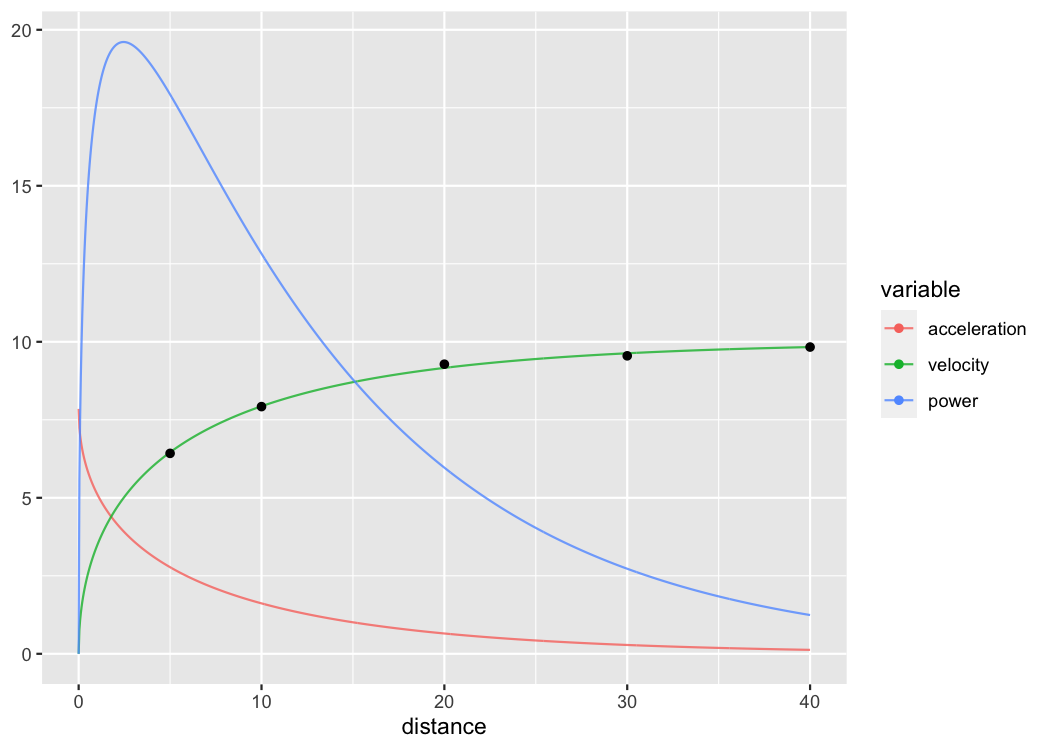
To estimate Force-Velocity profile using approach by Samozino et
al. (2016, 2022) use shorts::make_FV_profile():
kimberley_fv <- shorts::make_FV_profile(
MSS = kimberley_profile$parameters$MSS,
MAC = kimberley_profile$parameters$MAC,
# These are needed to estimate air resistance
bodymass = kimberley_bodymass,
bodyheight = kimberley_bodyheight
)
kimberley_fv
#> Estimated Force-Velocity Profile
#> --------------------------------
#> bodymass F0 F0_rel V0 Pmax
#> 6.0e+01 6.3e+02 1.1e+01 8.8e+00 1.4e+03
#> Pmax_rel FV_slope RFmax_cutoff RFmax Drf
#> 2.3e+01 -1.2e+00 3.0e-01 6.0e-01 -1.0e-01
#> RSE_FV RSE_Drf F0_poly F0_poly_rel V0_poly
#> 1.0e+00 9.5e-03 6.4e+02 1.1e+01 8.8e+00
#> Pmax_poly Pmax_poly_rel FV_slope_poly
#> 1.4e+03 2.3e+01 -1.2e+00
plot(kimberley_fv) +
theme_bw()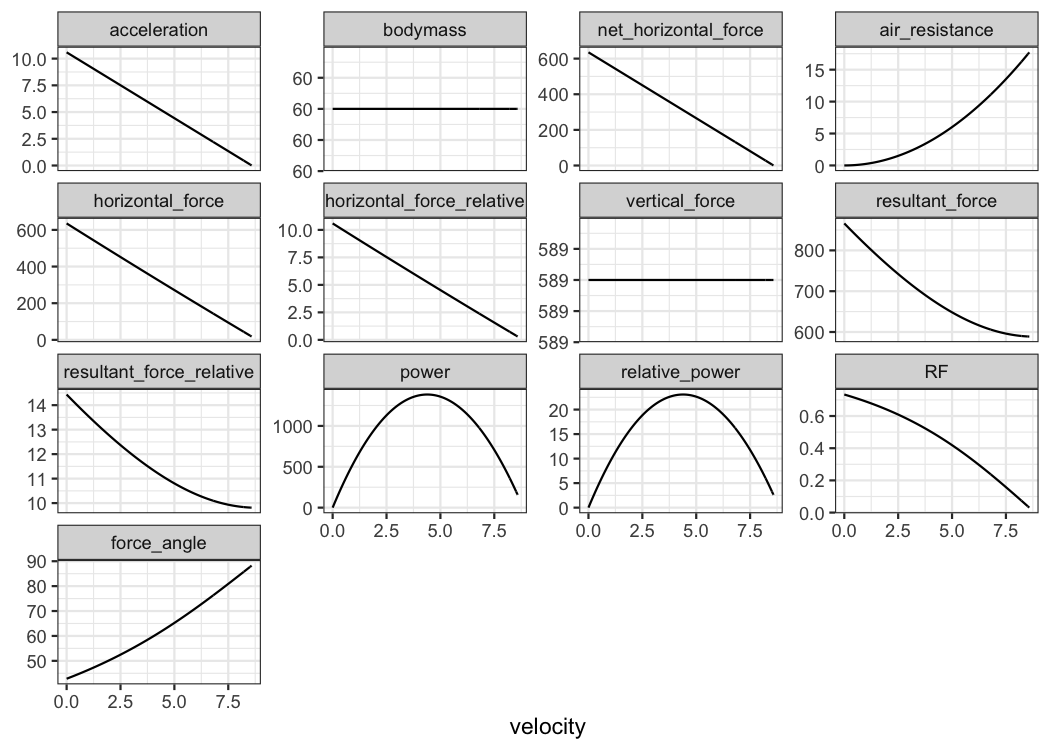
You have probably noticed that estimated MSS and TAU were a bit too high for splits data. Biased estimates are due to differences in starting positions and timing triggering methods for certain measurement approaches (e.g. starting behind first timing gate, or allowing for body rocking).
Here I will provide quick summary. Often, this bias in estimates is
dealt with by using heuristic rule of thumb of adding time correction
(time_correction) to split times (e.g. from 0.3-0.5sec; see
more in Haugen et al., 2012). To do this, just add time
correction to time split:
kimberley_profile_fixed_TC <- shorts::model_timing_gates(
distance = kimberley_data$distance,
time = kimberley_data$time + 0.3
)
kimberley_profile_fixed_TC
#> Estimated model parameters
#> --------------------------
#> MSS TAU MAC PMAX
#> 9.1 1.4 6.6 15.1
#>
#> Model fit estimators
#> --------------------
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> 0.0100 1.0000 -0.0077 0.0164 0.0164 0.0081 0.0064 0.2857
summary(kimberley_profile_fixed_TC)
#>
#> Formula: time ~ TAU * I(LambertW::W(-exp(1)^(-distance/(MSS * TAU) - 1))) +
#> distance/MSS + TAU
#>
#> Parameters:
#> Estimate Std. Error t value Pr(>|t|)
#> MSS 9.1278 0.0536 170.4 7.1e-09 ***
#> TAU 1.3776 0.0213 64.7 3.4e-07 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Residual standard error: 0.01 on 4 degrees of freedom
#>
#> Number of iterations to convergence: 5
#> Achieved convergence tolerance: 1.49e-08
coef(kimberley_profile_fixed_TC)
#> MSS TAU MAC PMAX
#> 9.1 1.4 6.6 15.1Instead of providing for TC, this parameter can be
estimated using shorts::model_timing_gates_TC().
kimberley_profile_TC <- shorts::model_timing_gates_TC(
distance = kimberley_data$distance,
time = kimberley_data$time
)
kimberley_profile_TC
#> Estimated model parameters
#> --------------------------
#> MSS TAU MAC PMAX TC
#> 8.97 1.23 7.27 16.31 0.23
#>
#> Model fit estimators
#> --------------------
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> 0.00113 1.00000 -0.00118 0.00121 0.00121 0.00080 0.00066 0.02824Instead of estimating TC, {shorts} package features a
method of estimating flying start distance (FD):
kimberley_profile_FD <- shorts::model_timing_gates_FD(
distance = kimberley_data$distance,
time = kimberley_data$time
)
kimberley_profile_FD
#> Estimated model parameters
#> --------------------------
#> MSS TAU MAC PMAX FD
#> 9.0 1.3 7.0 15.7 0.3
#>
#> Model fit estimators
#> --------------------
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> 0.00039 1.00000 -0.00040 0.00046 0.00046 0.00028 0.00024 0.00783model_timing_gates_() family of functions come with
LOOCV feature that is performed by setting the function parameter
LOOCV = TRUE. This feature is very useful for checking
model parameters robustness and model predictions on unseen data. LOOCV
involve iterative model building and testing by removing observation one
by one and making predictions for them. Let’s use Kimberley again, but
this time perform LOOCV:
kimberley_profile_LOOCV <- shorts::model_timing_gates(
distance = kimberley_data$distance,
time = kimberley_data$time,
LOOCV = TRUE
)
kimberley_profile_LOOCV
#> Estimated model parameters
#> --------------------------
#> MSS TAU MAC PMAX
#> 8.59 0.81 10.59 22.74
#>
#> Model fit estimators
#> --------------------
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> 0.034 1.000 -0.053 0.027 0.053 0.028 0.023 1.193
#>
#>
#> Cross-Validation
#> ------------------------------
#> Parameters:
#> # A tibble: 6 × 4
#> MSS TAU MAC PMAX
#> <dbl> <dbl> <dbl> <dbl>
#> 1 8.69 0.856 10.2 22.1
#> 2 8.60 0.815 10.5 22.7
#> 3 8.56 0.795 10.8 23.0
#> 4 8.57 0.797 10.8 23.0
#> 5 8.61 0.813 10.6 22.8
#> 6 8.39 0.760 11.1 23.2
#>
#> Testing model fit:
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> NA 0.999 -0.080 0.034 0.080 0.047 0.039 1.723Box-plot is suitable method for plotting estimated parameters:
LOOCV_parameters <- gather(kimberley_profile_LOOCV$CV$parameters)
ggplot(LOOCV_parameters, aes(y = value)) +
theme_bw() +
geom_boxplot() +
facet_wrap(~key, scales = "free") +
ylab(NULL) +
theme(axis.ticks.x = element_blank(), axis.text.x = element_blank())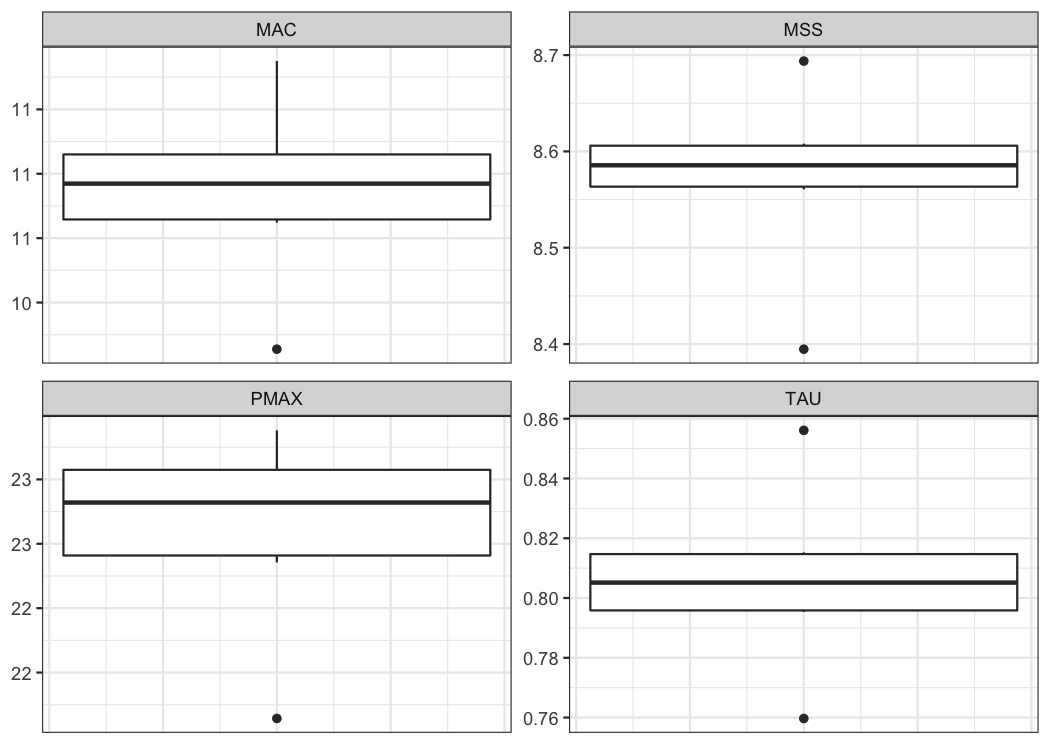
Let’s plot model LOOCV predictions and training (when using all data set) predictions against observed performance:
kimberley_data <- kimberley_data %>%
mutate(
pred_time = predict(kimberley_profile_LOOCV),
LOOCV_time = kimberley_profile_LOOCV$CV$data$pred_time
)
ggplot(kimberley_data, aes(x = distance)) +
theme_bw() +
geom_point(aes(y = time)) +
geom_line(aes(y = pred_time), color = "black") +
geom_line(aes(y = LOOCV_time), color = "red") +
xlab("Distance (m)") +
ylab("Time (s)")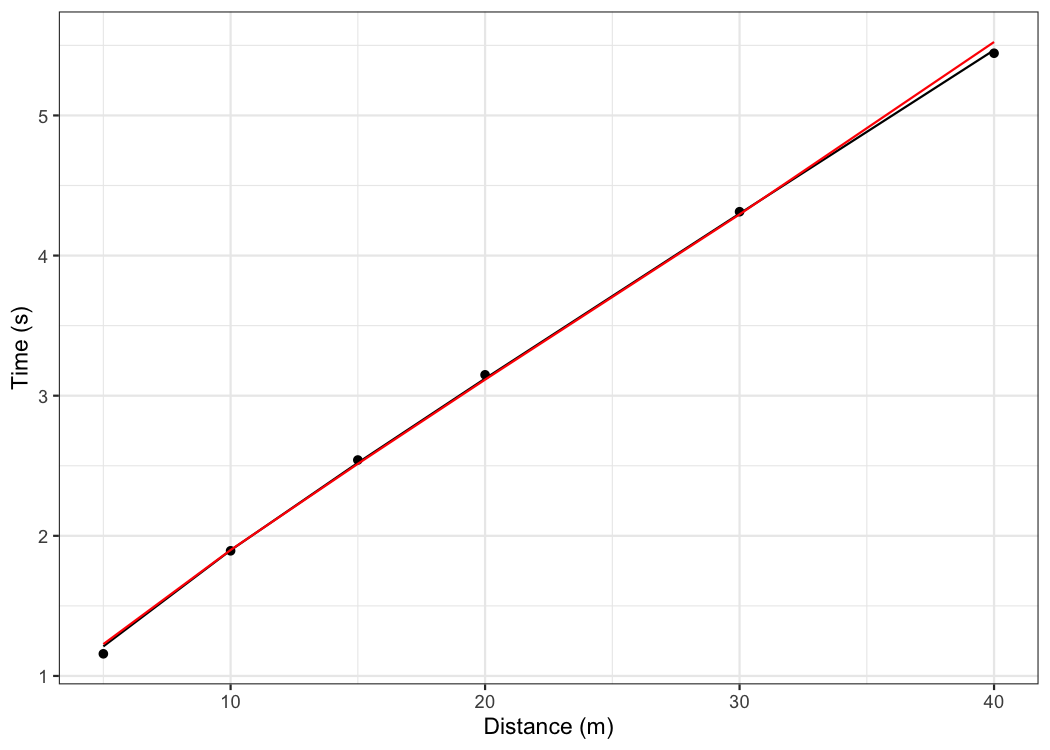
Let’s plot predicted velocity using LOOCV estimate parameters to check robustness of the model predictions:
plot_data <- kimberley_profile_LOOCV$CV$parameters %>%
mutate(LOOCV = row_number())
plot_data <- expand_grid(
data.frame(time = seq(0, 6, length.out = 100)),
plot_data
) %>%
mutate(
LOOCV_velocity = predict_velocity_at_time(
time = time,
MSS = MSS,
MAC = MAC
),
velocity = predict_velocity_at_time(
time = time,
MSS = kimberley_profile_LOOCV$parameters$MSS,
MAC = kimberley_profile_LOOCV$parameters$MAC
)
)
ggplot(plot_data, aes(x = time, y = LOOCV_velocity, group = LOOCV)) +
theme_bw() +
geom_line(alpha = 0.8) +
geom_line(aes(y = velocity), color = "red", size = 0.5) +
xlab("Time (sec)") +
ylab("Velocity (m/s)")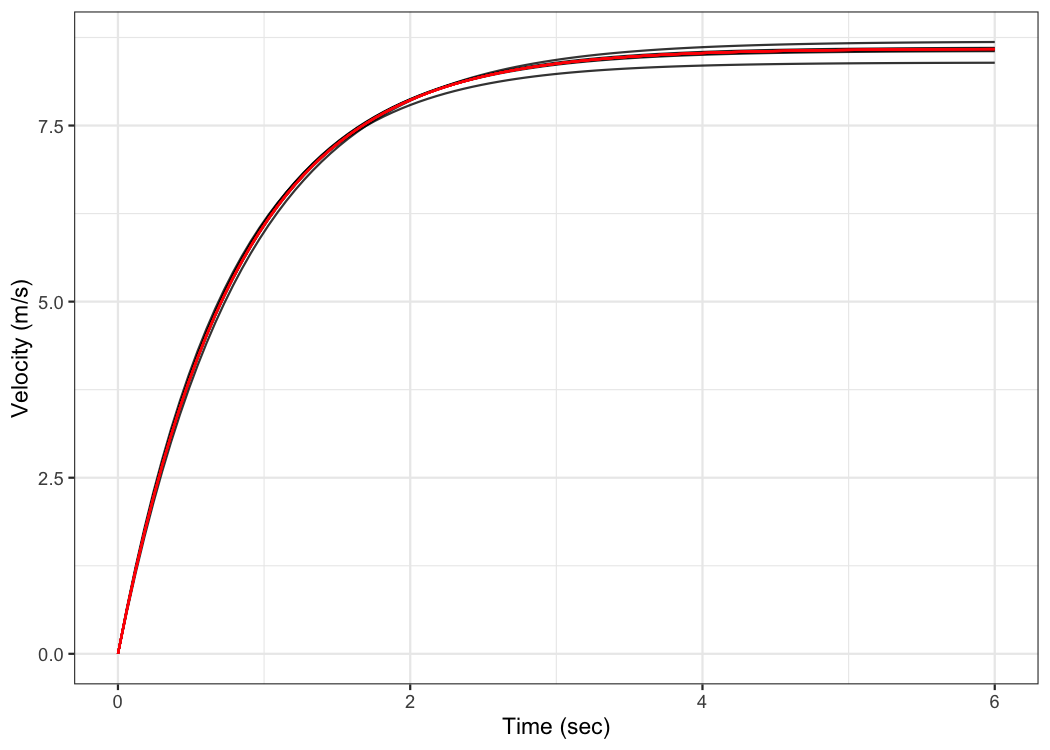
Cross-validation implemented in model_radar_gun()
function involves using n-folds, set by using CV=
parameter:
jim_profile_CV <- shorts::model_radar_gun(
time = jim_data$time,
velocity = jim_data$velocity,
CV = 10
)
jim_profile_CV
#> Estimated model parameters
#> --------------------------
#> MSS TAU MAC PMAX TC
#> 8.0e+00 8.9e-01 9.0e+00 1.8e+01 1.1e-04
#>
#> Model fit estimators
#> --------------------
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> 0.051 0.999 -0.164 0.151 0.164 0.051 0.039 Inf
#>
#>
#> Cross-Validation
#> ------------------------------
#> Parameters:
#> # A tibble: 10 × 5
#> MSS TAU MAC PMAX TC
#> <dbl> <dbl> <dbl> <dbl> <dbl>
#> 1 8.00 0.889 9.00 18.0 -0.0000351
#> 2 8.00 0.889 9.00 18.0 0.0000291
#> 3 8.00 0.889 8.99 18.0 0.000133
#> 4 8.00 0.888 9.01 18.0 0.0000355
#> 5 8.00 0.888 9.01 18.0 -0.000148
#> 6 8.00 0.888 9.00 18.0 0.000105
#> 7 8.00 0.889 8.99 18.0 0.000298
#> 8 8.00 0.890 8.99 18.0 0.000483
#> 9 8.00 0.890 8.99 18.0 0.000221
#> 10 8.00 0.888 9.00 18.0 -0.0000143
#>
#> Testing model fit:
#> RSE R_squared minErr maxErr maxAbsErr RMSE MAE MAPE
#> NA 0.999 -0.164 0.153 0.164 0.051 0.040 InfUsing the method outlined in Samozino et al (2022), one can find the optimal profiles, as well as the profile imbalance (compared to the optimal), for both sprint profiles (i.e., MSS and MAC) and Force-Velocity (FV). In addition to this, one can probe the profiles (i.e., increase V0/F0 or MSS/MAC for say 2.5% to check which improvement yield more improvement in sprint time). The following graph depicts estimate profile imbalances. Note that >100% is velocity deficit (i.e., increasing velocity; MSS or V0; will yield more improvement in sprint times), while <100% is force deficit.
MSS <- 10
MAC <- 8
bodymass <- 75
fv <- make_FV_profile(MSS, MAC, bodymass)
opt_df <- tibble(
dist = seq(5, 50, by = 5)
) %>%
mutate(
`Sprint Profile` = optimal_MSS_MAC(
distance = dist,
MSS,
MAC
)[["profile_imb"]],
`FV Profile` = optimal_FV(
distance = dist,
fv$F0_poly,
fv$V0_poly,
bodymass
)[["profile_imb"]],
`FV Profile (PeakPower)` = optimal_FV(
distance = dist,
fv$F0_poly,
fv$V0_poly,
bodymass,
method = "peak"
)[["profile_imb"]],
`Probe FV` = probe_FV(
distance = dist,
fv$F0_poly,
fv$V0_poly,
bodymass
)[["profile_imb"]],
`Probe MSS/MAC` = probe_MSS_MAC(
distance = dist,
MSS,
MAC
)[["profile_imb"]]
) %>%
pivot_longer(-dist, names_to = "profile")
opt_dist <- tibble(
`Sprint Profile` = find_optimal_distance(
MSS,
MAC,
optimal_func = optimal_MSS_MAC
),
`FV Profile` = find_optimal_distance(
fv$F0_poly,
fv$V0_poly,
bodymass,
optimal_func = optimal_FV
),
`FV Profile (PeakPower)` = find_optimal_distance(
fv$F0_poly,
fv$V0_poly,
bodymass,
optimal_func = optimal_FV,
method = "peak"
),
`Probe FV` = find_optimal_distance(
fv$F0_poly,
fv$V0_poly,
bodymass,
optimal_func = probe_FV
),
`Probe MSS/MAC` = find_optimal_distance(
MSS,
MAC,
optimal_func = probe_MSS_MAC
)
) %>%
pivot_longer(cols = 1:5, names_to = "profile")
ggplot(opt_df, aes(x = dist, y = value, color = profile)) +
theme_bw() +
geom_hline(yintercept = 100, linetype = "dashed", alpha = 0.6) +
geom_line() +
geom_point(data = opt_dist, aes(x = value, y = 100), size = 2) +
xlab("Distance (m)") +
ylab("Profile imbalance")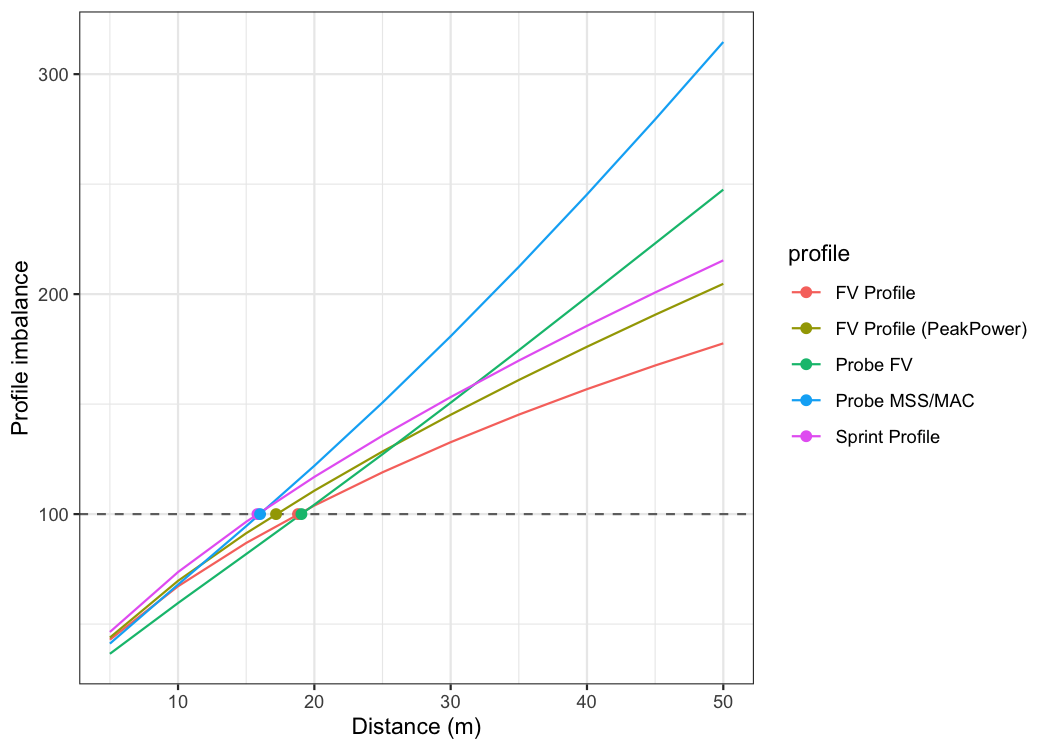
Jovanović, M., Vescovi, J.D. (2020). {shorts}: An R Package for Modeling Short Sprints. International Journal of Strength and Conditioning, 2(1). https://doi.org/10.47206/ijsc.v2i1.74
Vescovi, JD and Jovanović, M. (2021). Sprint Mechanical Characteristics of Female Soccer Players: A Retrospective Pilot Study to Examine a Novel Approach for Correction of Timing Gate Starts. Front Sports Act Living 3: 629694, 2021. https://doi.org/10.3389/fspor.2021.629694
Jovanovic M. (2022). Bias in estimated short sprint profiles using timing gates due to the flying start: Simulation study and proposed solutions. SportRxiv https://doi.org/10.51224/SRXIV.179
To cite {shorts}, please use the following command to get the BibTex entry:
citation("shorts")Please refer to these publications for more information on short sprints modeling using mono-exponential equation:
Chelly SM, Denis C. 2001. Leg power and hopping stiffness: relationship with sprint running performance: Medicine and Science in Sports and Exercise:326–333. DOI: 10.1097/00005768-200102000-00024.
Clark KP, Rieger RH, Bruno RF, Stearne DJ. 2017. The NFL Combine 40-Yard Dash: How Important is Maximum Velocity? Journal of Strength and Conditioning Research:1. DOI: 10.1519/JSC.0000000000002081.
Furusawa K, Hill AV, and Parkinson JL. The dynamics of” sprint” running. Proceedings of the Royal Society of London. Series B, Containing Papers of a Biological Character 102 (713): 29-42, 1927
Greene PR. 1986. Predicting sprint dynamics from maximum-velocity measurements. Mathematical Biosciences 80:1–18. DOI: 10.1016/0025-5564(86)90063-5.
Haugen TA, Tønnessen E, Seiler SK. 2012. The Difference Is in the Start: Impact of Timing and Start Procedure on Sprint Running Performance: Journal of Strength and Conditioning Research 26:473–479. DOI: 10.1519/JSC.0b013e318226030b.
Samozino P, Rabita G, Dorel S, Slawinski J, Peyrot N, Saez de Villarreal E, Morin J-B. 2016. A simple method for measuring power, force, velocity properties, and mechanical effectiveness in sprint running: Simple method to compute sprint mechanics. Scandinavian Journal of Medicine & Science in Sports 26:648–658. DOI: 10.1111/sms.12490.
Samozino P. 2018. A Simple Method for Measuring Force, Velocity and Power Capabilities and Mechanical Effectiveness During Sprint Running. In: Morin J-B, Samozino P eds. Biomechanics of Training and Testing. Cham: Springer International Publishing, 237–267. DOI: 10.1007/978-3-319-05633-3_11.
Samozino P, Peyrot N, Edouard P, Nagahara R, Jimenez‐Reyes P, Vanwanseele B, Morin J. 2022. Optimal mechanical force‐velocity profile for sprint acceleration performance.Scandinavian Journal of Medicine & Science in Sports 32:559–575. DOI: 10.1111/sms.14097.